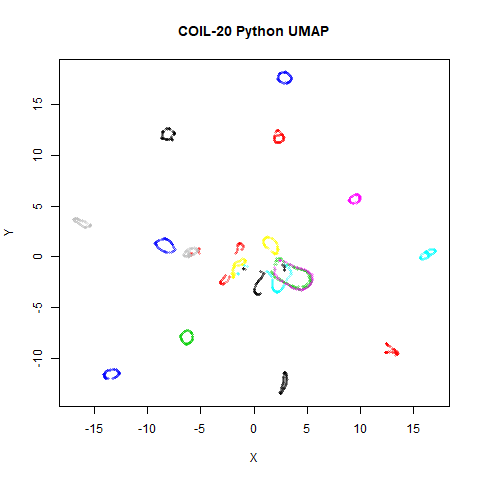
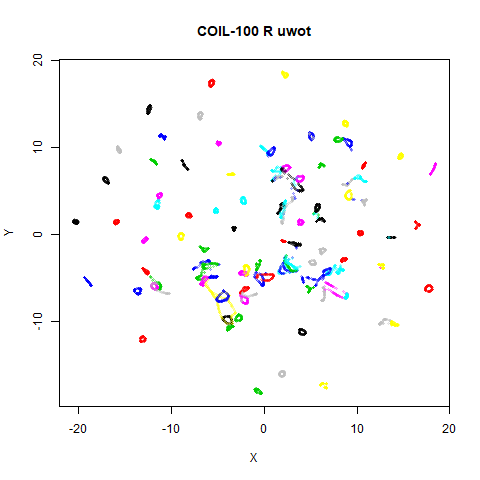
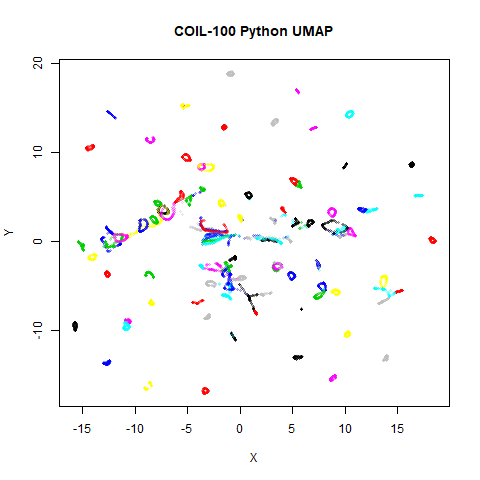
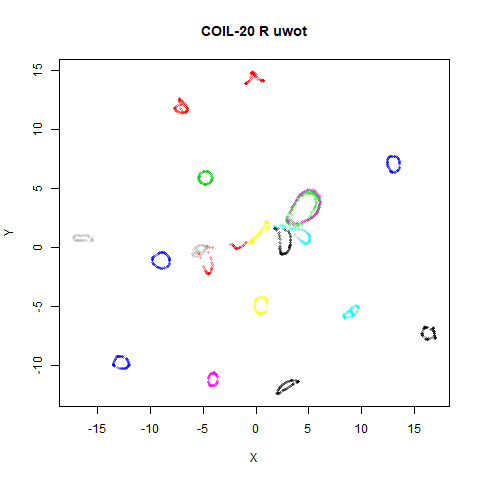Python Comparison

and some nearest neighbor comparisons

This page is a gallery of images comparing the output of uwot version 0.1.3 to the Python UMAP package version 0.3.8. In an ideal world, this wouldn’t be a very exciting document, as it would exist to demonstrate that uwot results resemble those from the Python implementation.

However, there are a couple of examples that highlight some differences between the implementations. It’s still not that exciting, but there may be some information of use to anyone using uwot and possibly some implications for users of t-SNE packages. To distinguish between the general technique of UMAP and the its specific implementation in the Python package of the same name, I’ll refer to the Python implementation with the formatting UMAP.

For details on the datasets, see the UMAP examples gallery. The uwot results have been re-run for the images here using different random seeds, but they should resemble the uwot output on that page.

The datasets originated in R, mostly being loaded via the snedata package. I then exported them to CSV, before reading them into Python. UMAP version 0.3.8 was used to generate the embeddings, using all default settings. The embeddings were then written to CSV and read back into R for visualization.

The uwot output also used default settings with the following exceptions: pca = 100 was used to reduce the dimensionality to a maximum of 100 columns (data was mean-centered as part of this process, but not rescaled), because the Annoy nearest neighbor search can be very slow for high-dimensional data. UMAP’s nearest neighbor search seems less affected by dimensionality. Also, min_dist = 0.1, which is the default for the Python UMAP. uwot uses a default of min_dist = 0.01. Why? I would love to tell you, but I think I just made a mistake when I set the uwot defaults. Therefore, the defaults will probably change in some later version of uwot. Fortunately, this doesn’t make a perceptible practical difference, but I will use the Python default of min_dist = 0.1 in the following results.

There is also a potential difference in initialization. Both packages use a spectral initialization if possible, but differ if the input graph contains more than one component: UMAP attempts a meta-embedding of the two separate components, where uwot abandons a spectral approach and falls back to using PCA (followed by rescaling the output to a standard deviation of 1 for each axis). This affects the following datasets: iris, coil20, coil100, norb and tasic2018.

set.seed(42)
iris_umap <- umap(iris, pca = 100, min_dist = 0.1)

# iris X data read from CSV
iris_umap = umap.UMAP().fit_transform(iris_x)

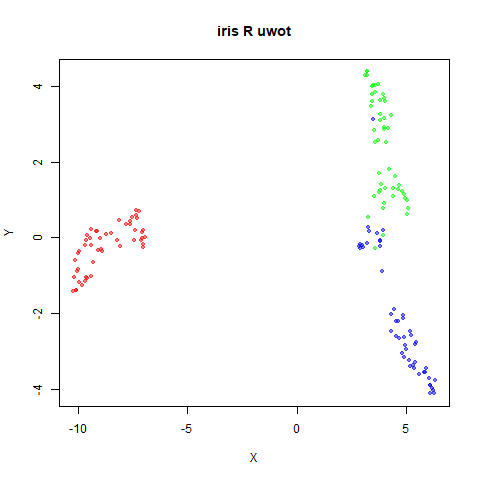
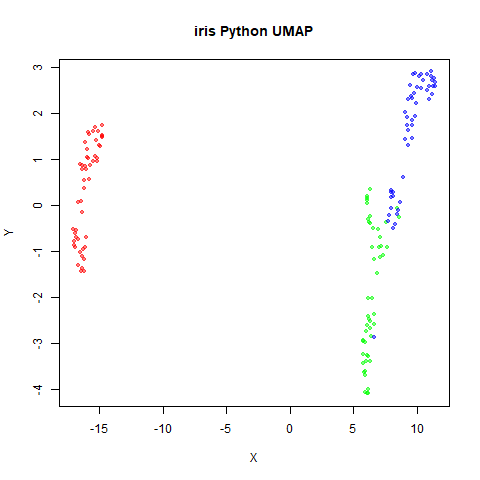
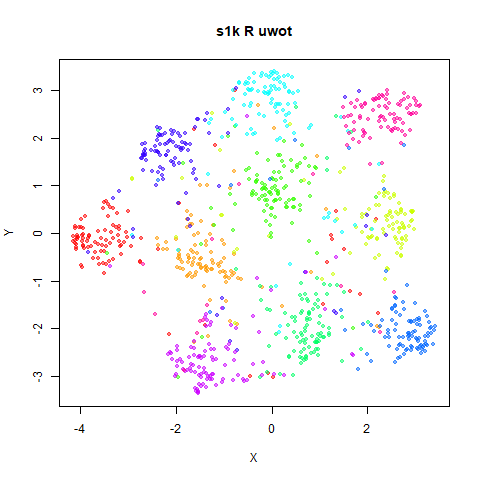
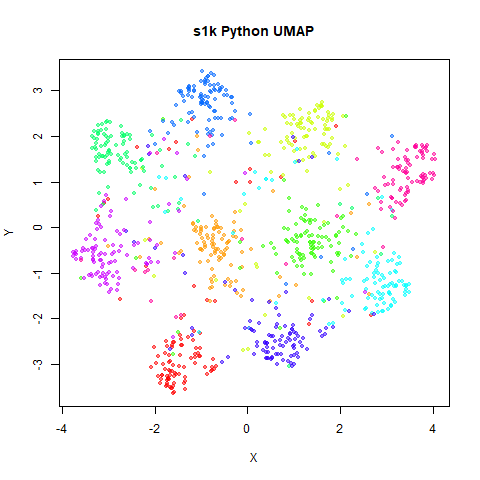
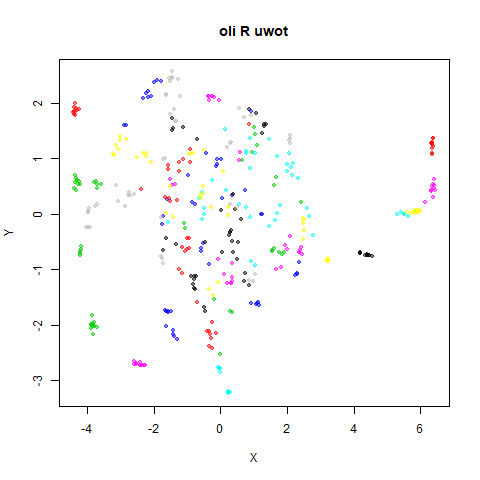
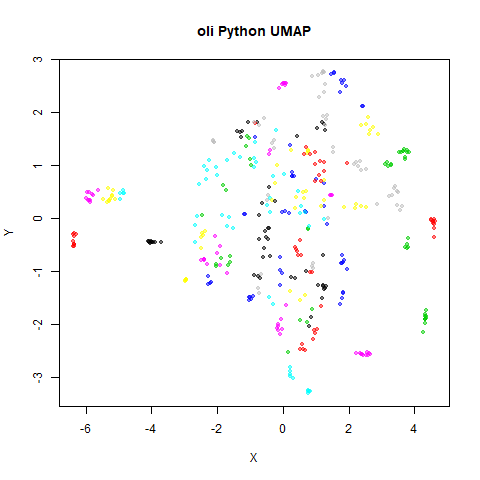
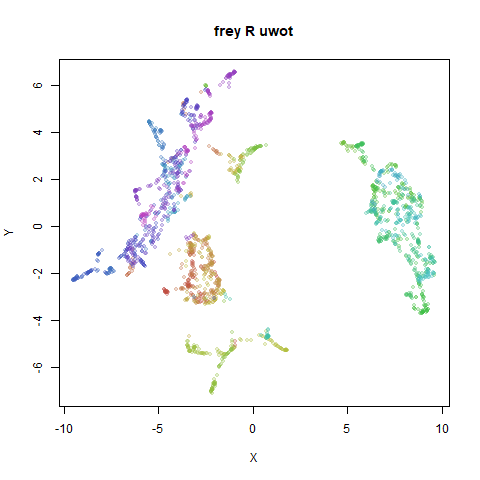
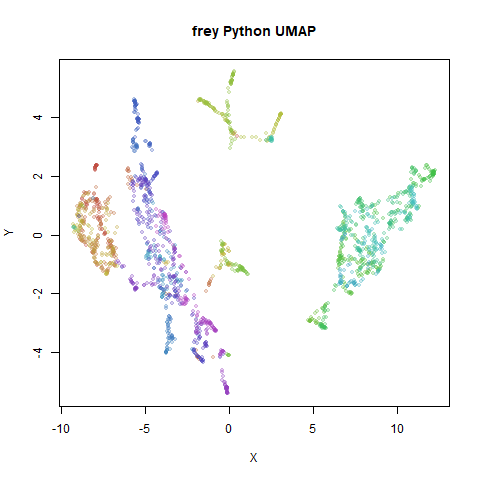
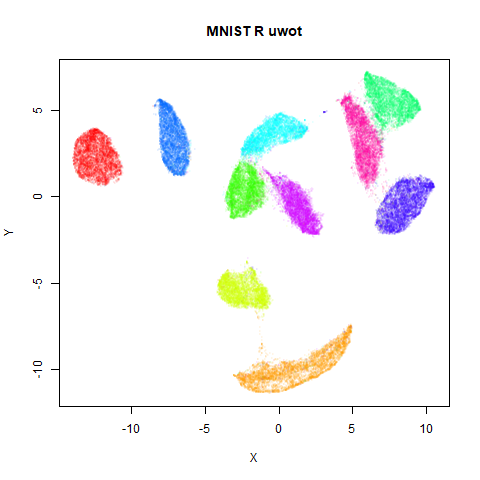
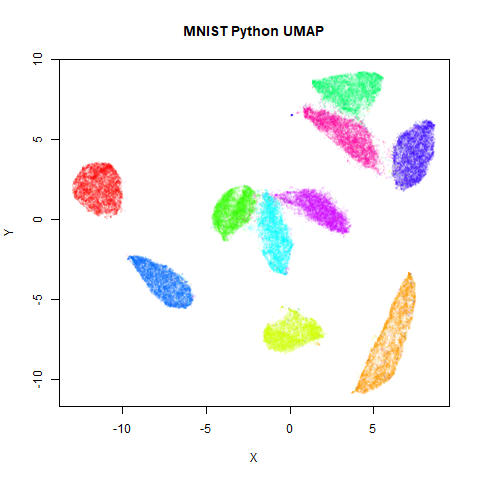
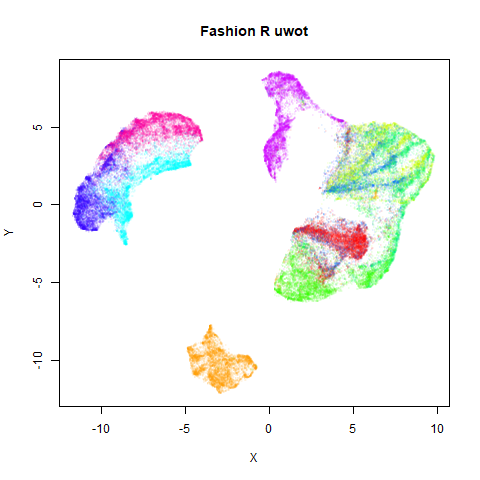
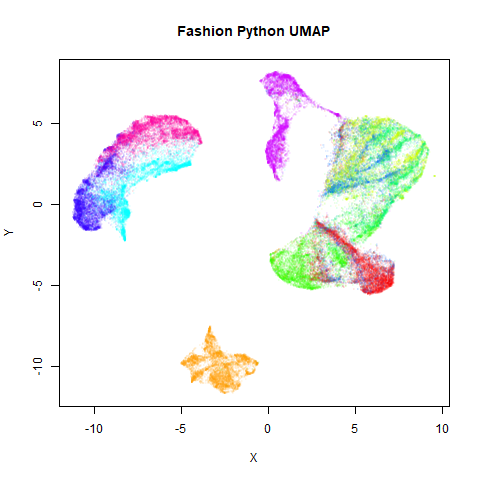
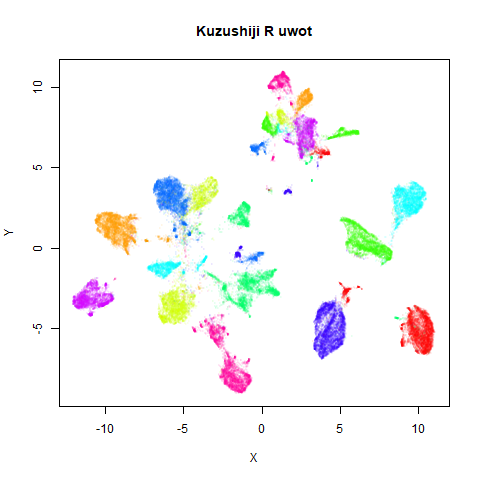
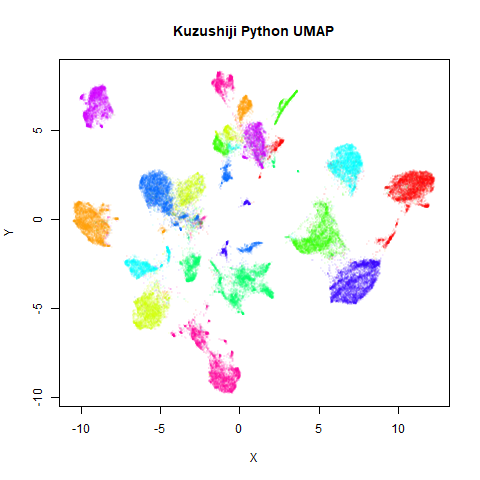
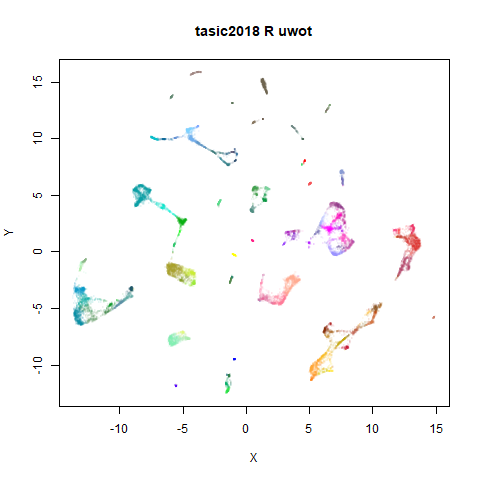
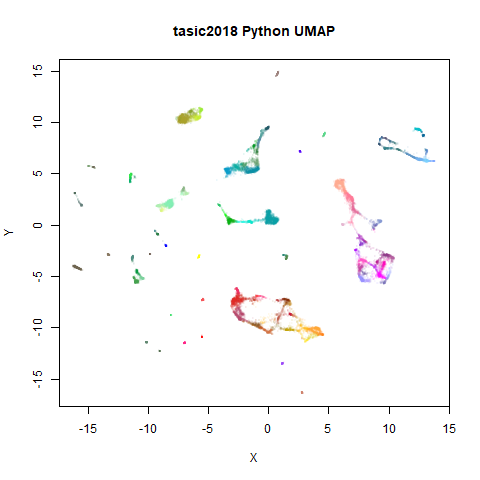
Below the results on the left are for the uwot output. The image on the right is from UMAP. I present most of these results without comment because they seem to be very similar to each other. There are two exceptions, for the small NORB dataset (norb) and the gene expression dataset macosko2015, which will be discussed in their section.

Results

iris

s1k

oli

frey

coil20

coil100

mnist

fashion

kuzushiji

norb

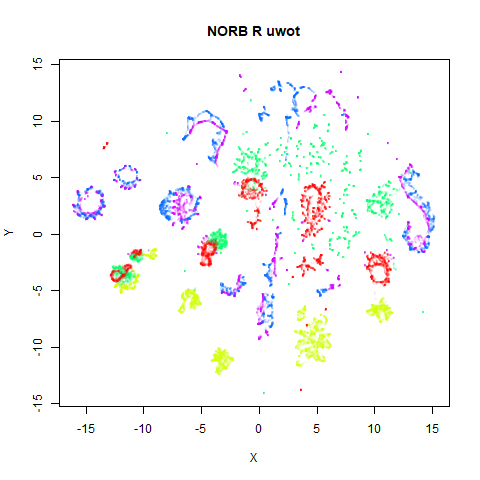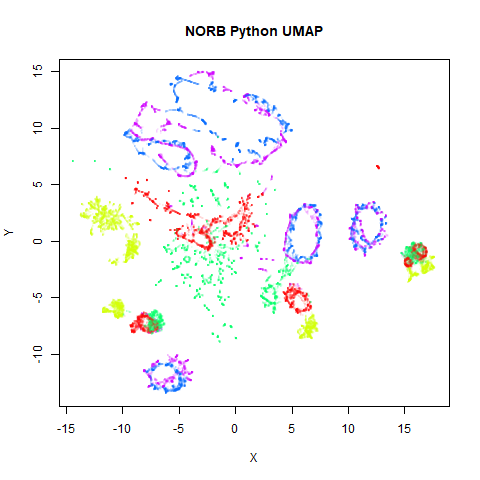Here’s a result that seems worth commenting on. The uwot results show slightly less structure, a large blue loop seems to have been broken up.

I suspect that the PCA preprocessing to 100 dimensions as used by uwot is too aggressive here and might be throwing away too much of the variance in the dataset. Compared to the ground truth 15 nearest neighbors using FNN, Annoy results with pca = 100 are 82% accurate. Without PCA, this accuracy goes up to 99% and the uwot results are much closer to the UMAP results. This is the image below, on the left. Meanwhile, if you use the PCA results as input to UMAP, the output now looks a bit more like the uwot results. That’s the image on the lower right.

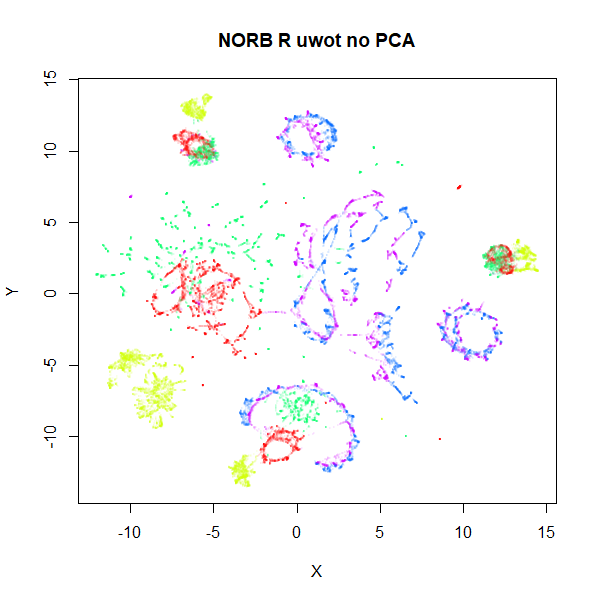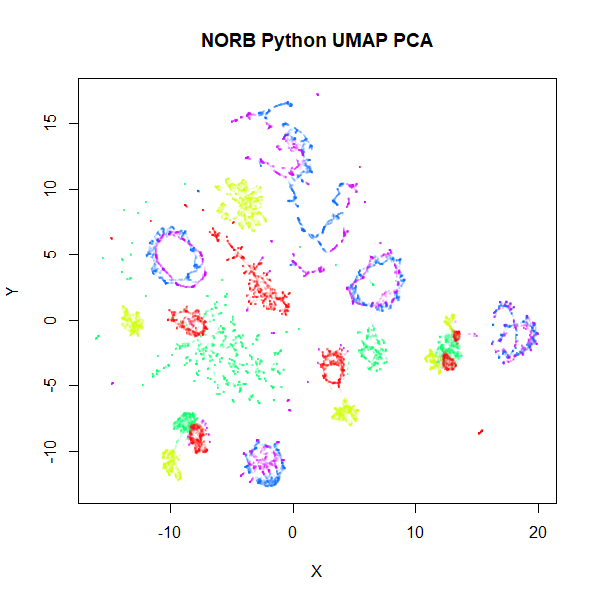Unfortunately, the very high dimensionality of norb makes running Annoy on it directly very slow indeed: with a single-thread, it took 4 and a half hours, versus around 5 minutes in the PCA case. We will revisit nearest neighbor accuracies later.

Note also that norb is one of the datasets where the graph contains two separate components, so the initialization of the output coordinates is different between uwot and UMAP, with UMAP’s “meta-embedding” approach better at retaining local structure.

tasic2018

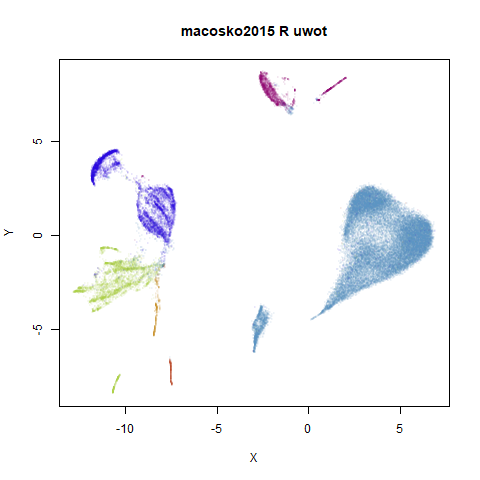
macosko2015

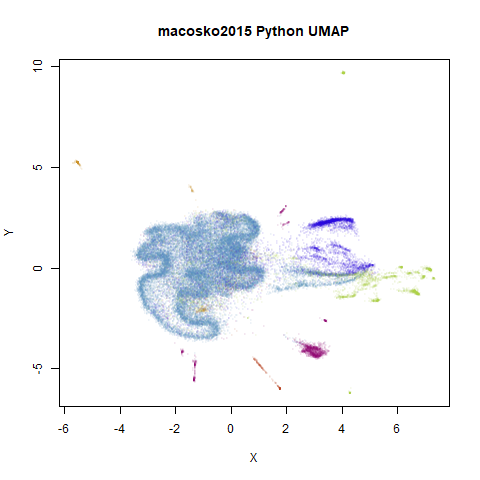This result shows the largest deviation of uwot from UMAP. That big cyan cluster is of an obviously different shape in the two plots. The source of the difference here seems to be nearest neighbor results. It turns out that both uwot and UMAP have trouble find good approximations to the nearest neighbors with this dataset, but UMAP does a lot better. We will get into more detail about the nearest neighbor accuracies across the datasets in the next section. For now, below are two further plots. 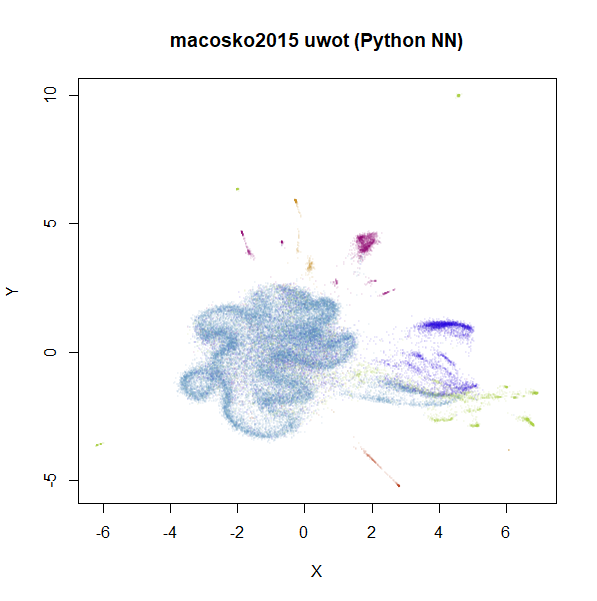The left-hand plot is the uwot results when it uses the more accurate nearest neighbor data calculated by UMAP: the uwot results now resemble the UMAP results, which is reassuring. The right hand plot uses exact nearest neighbor results calculated via the FNN.

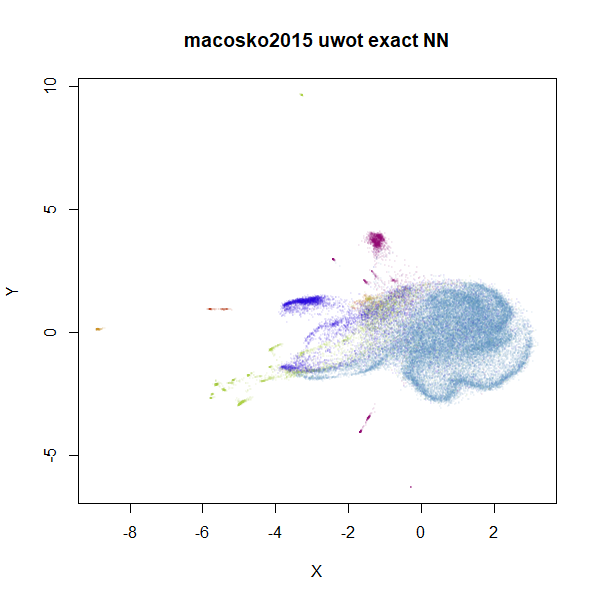Even though the UMAP nearest neighbor data is better than that which uwot produced, we can still see an obvious difference in the two plots, so it’s clear that this data set presents a challenge for the approximate nearest neighbor methods considered here.

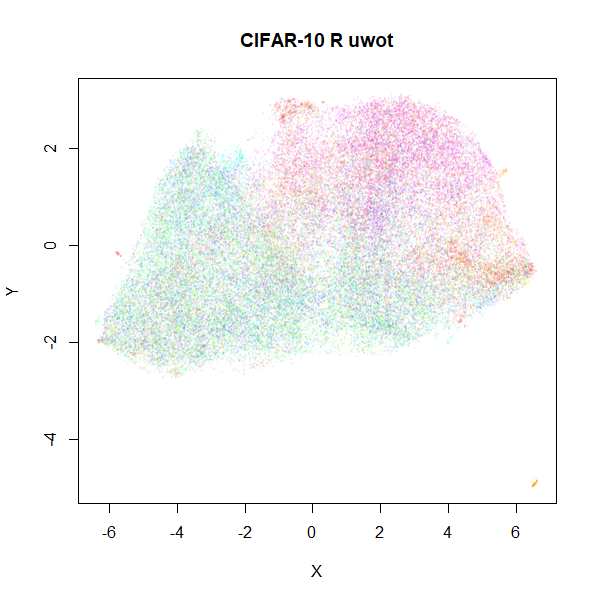
cifar10

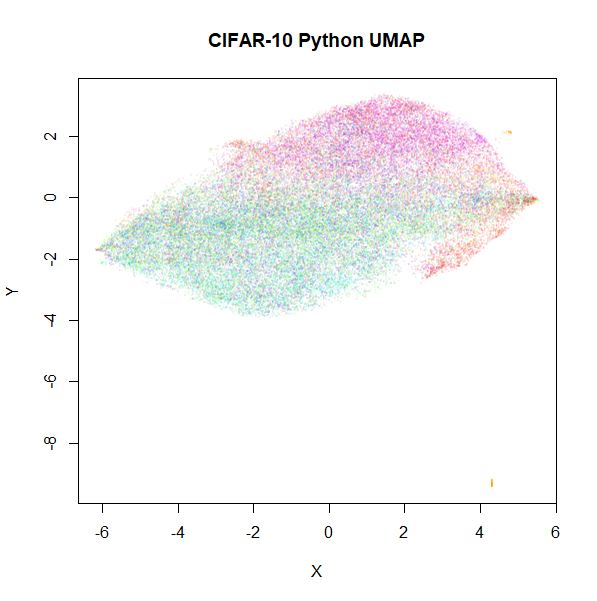Based on results with this dataset in the UMAP examples gallery, I wasn’t expecting these results to be a feast for the eyes. After seeing the difference in results with macosko2015, I am just relieved that these two results look disappointing in a similar way.

Nearest Neighbor Accuracy

The norb and macosko2015 results suggest that the use of PCA and the nearest neighbor search methods present the biggest source of difference between uwot and UMAP. Here are some more details.

For small datasets, which in both implementations means less than 4,096 observations, both uwot and UMAP calculate the exact nearest neighbors. For larger datasets, uwot uses the Annoy method, and UMAP uses pynndescent, which uses random projection trees, followed by nearest neighbor descent.

For the larger datasets, I used the FNN package to generate the exact 15 nearest neighbors and then compared results for uwot and UMAP. For UMAP, I used default settings. For uwot, I applied pca = 100 as that is what I currently use for high dimensional datasets. The third column shows the amount of variance explained by only keeping 100 components.

datasets	uwot	UMAP	PCA 100 var
coil100	89.1%	99.7%	88.4%
mnist	86.2%	97.5%	91.5%
fashion	74.3%	97.9%	91.2%
kuzushiji	78.3%	95.2%	84.6%
norb	81.7%	98.3%	95.6%
tasic2018	48.0%	97.7%	67.7%
macosko2015	11.2%	41.8%	37.3%
cifar10	67.4%	84.1%	90.1%

UMAP does a pretty incredible job with nearly every dataset, and it’s fast too. And it doesn’t need to use PCA to reduce the dimensionality. The obvious exception is macosko2015. I was unable to find a combination of parameters with pynndescent that produced good results, e.g. by increasing the number of trees in the RP tree initialization or the number of iterations in the nearest neighbor descent phase. With n_trees=250, I was able to get to 54.9% accuracy, but I started to get out of memory errors much beyond this setting, and nearest neighbor descent tends to converge after 5-6 iterations anyway. Doing better will may require more manipulation of the sampling rate and candidate list size used in nearest neighbor descent, which can quickly cause a large increase in memory and run time if you aren’t careful. Also, you can’t fiddle with these parameters in UMAP version 0.3.8 anyway.

uwot results… well, they’re less impressive than UMAP’s. The tasic2018 results are pretty bad, and the macosko2015 results can be fairly described as horrendous. The accuracies show a rough correlation with the percentage of variance explained by 100 components. Results for tasic2018 and especially macosko2015 show that 100 components may not be enough to extract the meaningful variation from the datasets, which might explain the inability to find the true nearest neighbors. The uwot defaults for the Annoy search are somewhat arbitrary, having been copied from LargeVis. That package used nearest neighbor descent to improve the accuracy, and increasing Annoy’s n_trees parameter can give a small improvement to some of the datasets, but the increase in computation time is probably not worth the small increase in accuracy I’ve seen when trying this. It seems that in cases where the current defaults don’t work well, it’s because too much information is thrown away by the PCA pre-processing.

tasic2018 and macosko2015 are both transcriptomics datasets and clearly represent an interesting challenge to Annoy, while macosko2015 troubles even pynndescent. The other datasets are image datasets. Possibly the way the data has been scaled and prepared for these biology datasets makes life harder for approximate nearest neighbors? 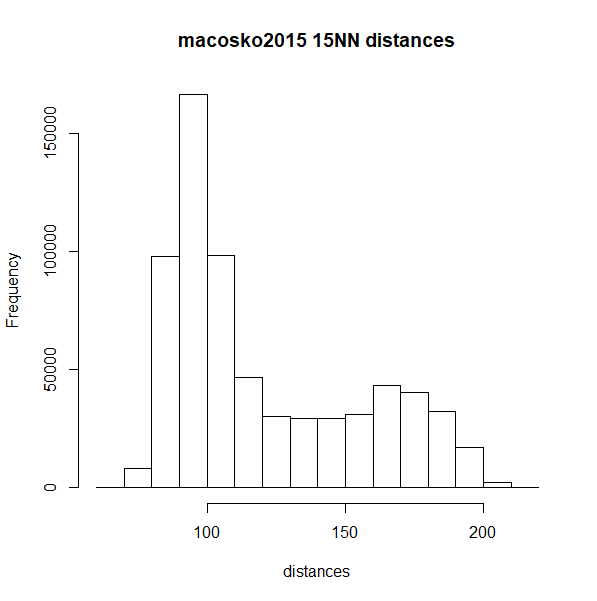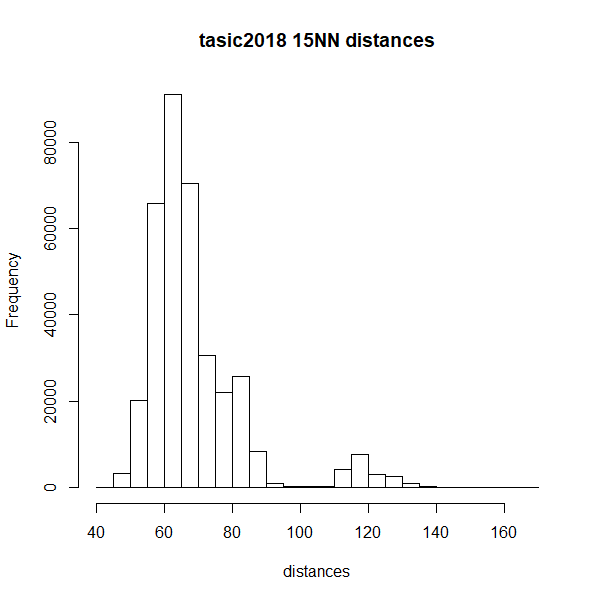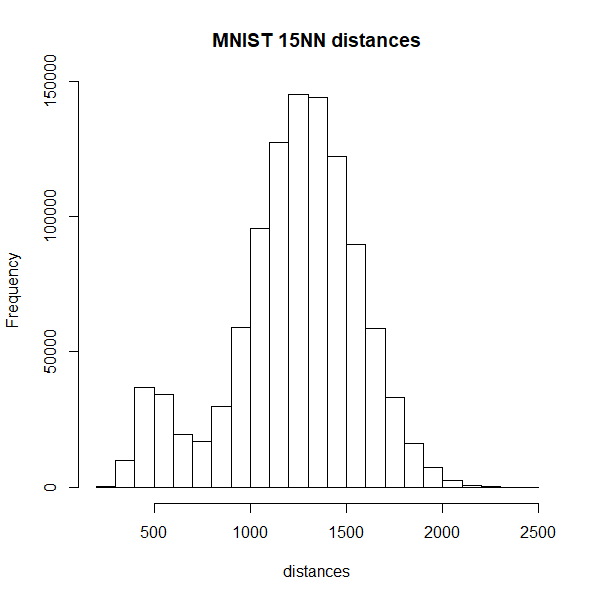It’s hard to know where to start when it comes to unpicking what causes macosko2015 to perform so differently, but here is a histogram of the nearest neighbor distances for macosko2015 and tasic2018 (top row), which misbehave with Annoy, and on the bottom row are the histograms for mnist and fashion, which are better behaved:

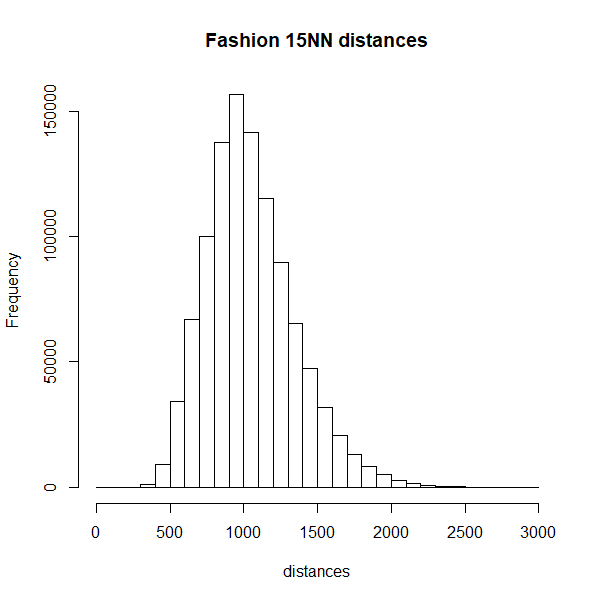The biomodal distribution of macosko2015 and tasic2018 do seem more similar to each other than they do to mnist or fashion. That said, tasic2018 behaves perfectly well with the pynndescent method, so I see no obvious answers here.

Conclusions

The good news is that for most datasets, the differences between uwot’s UMAP implementation and that of the Python UMAP implementation makes very little difference. The bad news is that there are a couple of cases where we see differences. The biggest offender is macosko2015 but there neither method is doing a perfect job. Nonetheless, UMAP is able to calculate nearest neighbors more accurately and more quickly than uwot.

One source of the difference is the use of Annoy as the nearest neighbor calculation method. It does seem to be solidly slower than pynndescent, but in my experience, it can reach high accuracies. even if it takes a while. March 8 2020: On Windows, there used to be an issue where an Annoy index that was larger than 2GB on disk couldn’t be read back in. Make sure you are using a version of RcppAnnoy 0.0.15 or later to avoid this.

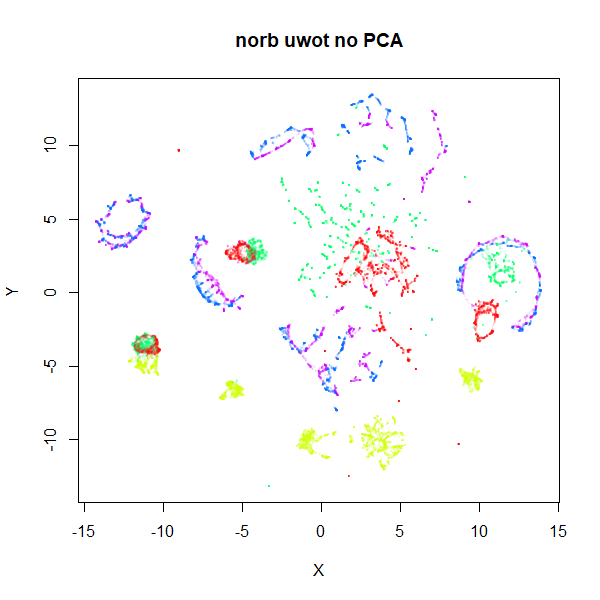
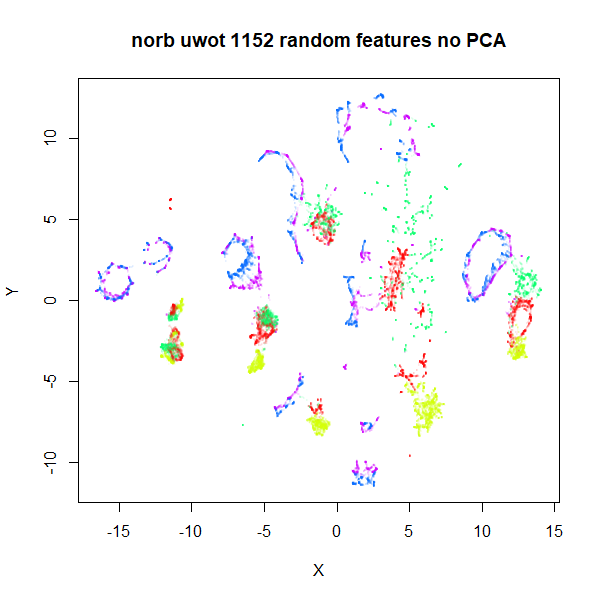
The time to search an Annoy index seems to start scaling quite badly with dimensionality > 1000, so if you can get away with picking 500-1000 random features and use that, you could try that. With 1,152 random features (i.e. 1/16th the pixels innorb), visual results aren’t that much worse with this approach and the nearest neighbor search runs 100 times faster (50 minutes vs 20 seconds):

Otherwise, if you have a high-dimensional dataset, you should consider PCA. I don’t have any solid advice for the number of components to retain if you do use PCA for preprocessing. Less than the usual t-SNE default of 50 is probably unwise. I use pca = 100 in most examples, but as we’ve seen, that can still sufficiently perturbs the pairwise distances in the input data to give some differences in the output. It would be nice if you could use more components to get a better trade-off of accuracy and speed, but even with fast partial PCA routines used by uwot (courtesy of irlba), extracting more than 100 components can be quite time-consuming.

What about t-SNE?

uwot is not the only dimensionality reduction to use PCA or Annoy for approximate nearest neighbor search. LargeVis uses it, the t-SNE package Fit-SNE has Annoy as an option and openTSNE seems to have at least considered it (see e.g. https://github.com/pavlin-policar/openTSNE/issues/28). It is also standard practice in t-SNE to reduce dimensionality: Rtsne, a wrapper around the de-facto standard Barnes Hut t-SNE routine. will only keep 50 components via PCA by default.

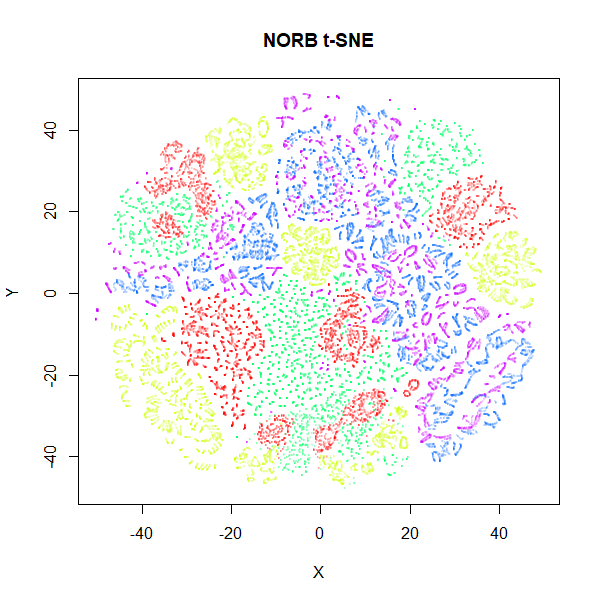
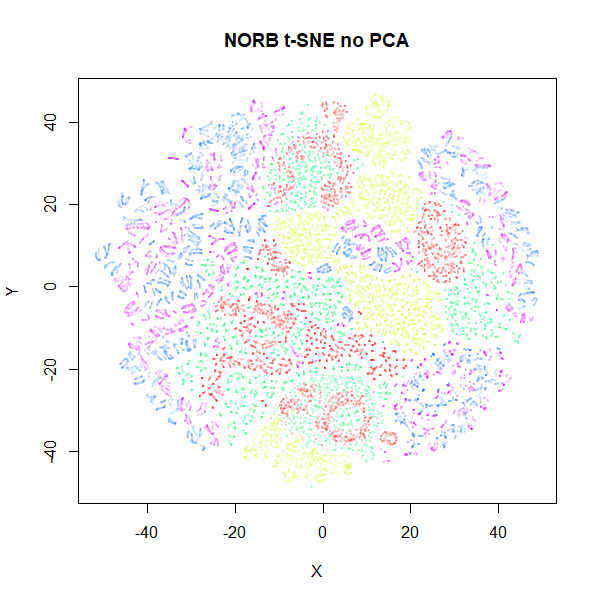
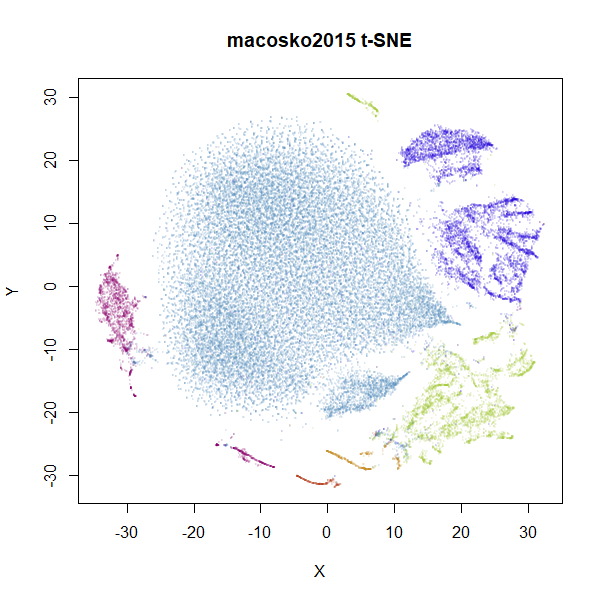
Does the PCA issue effect t-SNE? Well, a little bit. Below are results for norb and macosko2015 (openTSNE’s documentation is where I discovered this dataset, as it happens) with t-SNE results from Rtsne, using perplexity = 15. The images on the left use PCA to reduce the initial dimensionality down to 100, while the ones on the right use the raw input data.

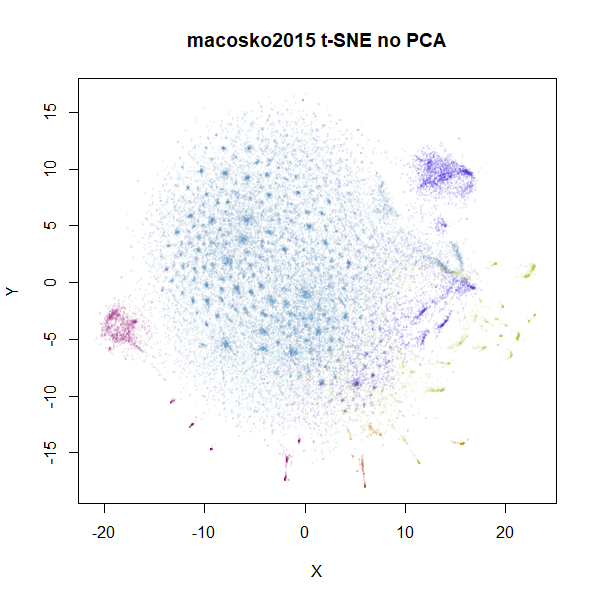norb results seem fairly unaffected, but we also see for macosko2015 that there’s a change to the main large cluster. Usually, you don’t set perplexity as low as 15, so are there also differences when the perplexity is set to a more typical value, like 50? Also, the default PCA dimensionality setting in Rtsne is 50, not 100, so here are those t-SNE plots repeated with perplexity = 50 and either pca = TRUE, partial_pca = TRUE, initial_dims = 50 on the left, and pca = FALSE on the right:

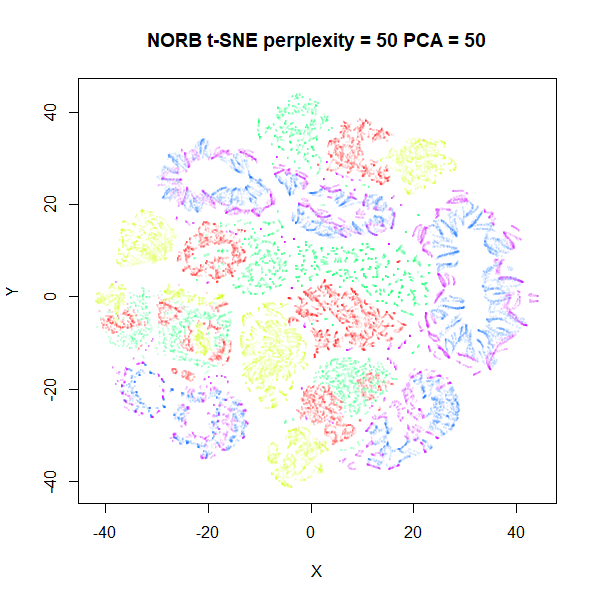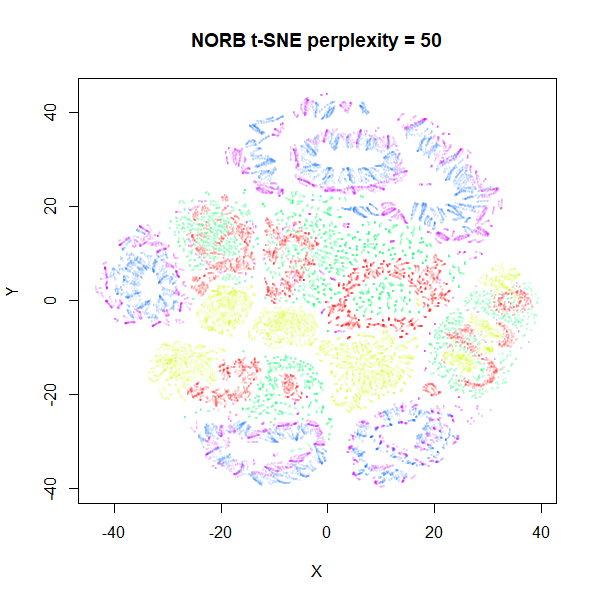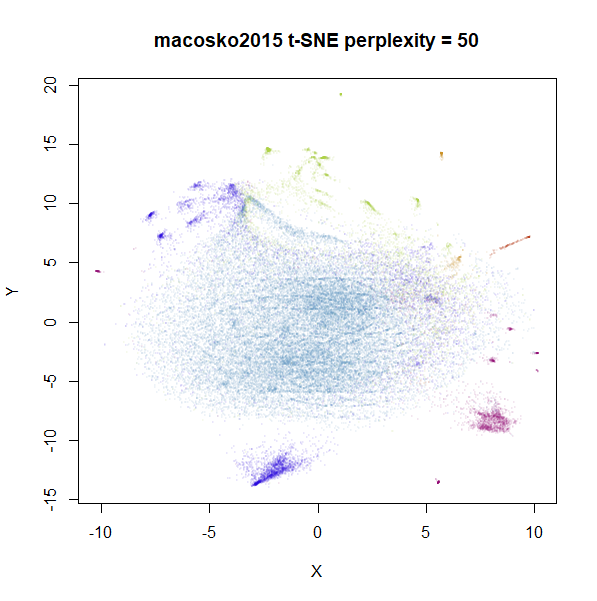Again, the norb dataset is less affected than macosko2015 but for the latter there is a definite effect of preprocessing with PCA. This is something to bear in mind before applying PCA to your data even with t-SNE. On balance, I’d probably live with the effect of applying PCA to your data, because just like with uwot, Rtsne input processing can take a few hours with very high dimensional datasets.

Finally, some people consider results obtained with PCA to be more reliable than those using the “raw” input, because PCA can be considered a way to denoise data, where the lower-variance components are assumed to be irrelevant. I might be a bit biased, but of all the UMAP plots of macosko2015, I think the default uwot one shows the best separation of clusters, so maybe there’s something to it. But this is also the reason I tabulated the amount of variance 100 components explained for each dataset. Where most of the datasets keep a large majority of the variance with 100 components, in the case of macosko2015, you would have to be prepared to argue why it was ok to throw away over 60% of variance in the data. I’m sure it can be done, but you would need a solid, ideally biology-based justification.

A future version of uwot will hopefully contain an implementation of nearest neighbor descent optimization to reduce the gap in nearest neighbor accuracy with UMAP.