PaCMAP Comparison

Introduction

PaCMAP (paper, repo) is a highly-regarded dimensionality method, firmly in the LargeVis/UMAP family. It’s main point of differentiation from related methods is that it balances local and global structure without needing to tune hyperparameters. The PaCMAP authors’ blog post explicitly states:

PaCMAP has no parameters that are designed to be tuned.

Bold words! Also PaCMAP is pretty fast.

Alas there is no native R package for PaCMAP (as far as I know). You can of course call it via reticulate, and the PaCMAP repo has a notebook demonstrating that. But that’s a bit unsatisfactory. I have spent a lot of time studying the Python code and you can see my notes on the method if you want the details. The upshot of all that is that I feel qualified to say that it would actually be quite hard to integrate PaCMAP into uwot.

Turning UMAP into PaCMAP?

But can we bend UMAP to make it behave more like PaCMAP? Here is a very high-level overview of the most important ways that PaCMAP differs from UMAP:

Nearest neighbors are chosen using a method originating in self-tuning spectral clustering and also used in Trimap. This rescales some nearest neighbor distances based on local densities. This doesn’t seem to make a massive difference in results in my testing so I won’t worry about implementing it.
There is a special class of “mid-near” items, which are points further away than nearest neighbors but closer than randomly-sampled pairs. In the language of contrastive learning, you can think of these as “semi-positive” examples. Use of these mid-near pairs requires introducing a new loss term and gradient type, which is the main problem with integrating PaCMAP into uwot. Plus there are different weights applied to each component of the loss which changes during the optimization process. This would require even more reworking of uwot. Fortunately, it seems like most of the benefit of this (and using mid-near items in general) is when you initialize the embedding randomly. Let’s just not do that.
The negative examples for each item are are sampled once and then re-used for all epochs, unlike UMAP which is always selecting different vertices. We’re also not going to do this as this is probably just a speed optimization rather than necessary for the working of the method as a whole.
By default, if your input data has more than 100 columns, then Truncated SVD is applied to reduce the dimensionality to 100. I’m not really a fan of this as a default setting, but we can easily implement it by setting pca = 100. It does seem to be an important part of PaCMAP’s speed improvements too.
Initialization is with PCA, which is also easily implemented in uwot with init = "pca". PaCMAP then shrinks this by multiplying all the coordinates by 0.01. This is supported by setting init = "pacpca" if you really want to do it, but I don’t think it’s necessary (or actually that good an idea).
The loss function and gradient for PaCMAP are rather different from UMAP. In general these are more gentle than UMAP’s and cause less tearing and twisting of any manifold structure in the embedded coordinates. But in most real-world datasets I have looked at, there isn’t a huge effect from the gradient.

So from all of the above you can see that there are some reasonable changes between UMAP and PaCMAP and most of my responses have been “yeah, I don’t fancy changing that”. So to put my cards on the table, I think the major source of differences between UMAP and PaCMAP are:

Using PCA as initialization (this is the most important difference).
Using PCA to reduce high-dimensional data to 100 dimensions.

Methods

To make this simple I used:

PaCMAP with its default settings. I used Python 3.12 and PaCMAP 0.7.3. There have been some patch releases since then, but it has no meaningful effect on the results shown here.
For UMAP, I used default umap2 parameters. HNSW was used as the nearest neighbor method.

I didn’t make any effort to match number of neighbors or number of epochs and so on. I think these are all pretty comparable with their default settings.

PCA was performed using irlba. To make results easier to compare, the output coordinates were rigid-body rotated to align with the PCA results using the Kabsch algorithm (the coordinates were also additionally flipped along one dimension, and the result with lowest error was chosen).

Datasets

I tried to use a variety of datasets, including many used by the PaCMAP authors in their paper and blog-post. Many of these had Python code in the PaCMAP repo which was very useful. See the examples article for more details on the datasets.

One extra dataset that we will also look at is curve2d, a simple 2D curve. This is used as an example in the paper of how even if you start with the original coordinates scaled by a constant, dimensionality reduction methods will, rather than do nothing, still distort the overall shape. Python code to generate the curve is at https://github.com/YingfanWang/PaCMAP/blob/master/experiments/run_experiments.py.

Results

There’s a table of embeddings below. ased on my feelings that PCA is the key to a lot of PaCMAP’s differences to UMAP, I have three different settings of UMAP. From left to right the settings used were:

UMAP with its default parameters (UMAP).
UMAP initialized with PCA (UMAP PCA), i.e. init = "pca".
UMAP with the input data reduced to 100 dimensions via PCA, if it had more than 100 columns (UMAP-PCA100) and also initialized with PCA, i.e. init = "pca", pca = 100.

Finally on the right are the embeddings from running PaCMAP.

I made no special effort to account for variability between runs for either UMAP or PaCMAP. Based on having run these many, many times, I am confident that the results are representative of the methods’ performance.

If you have javascript enabled, you can click on any image to embiggen it.

Dataset	UMAP	UMAP PCA	UMAP PCA100	PaCMAP
curve2d
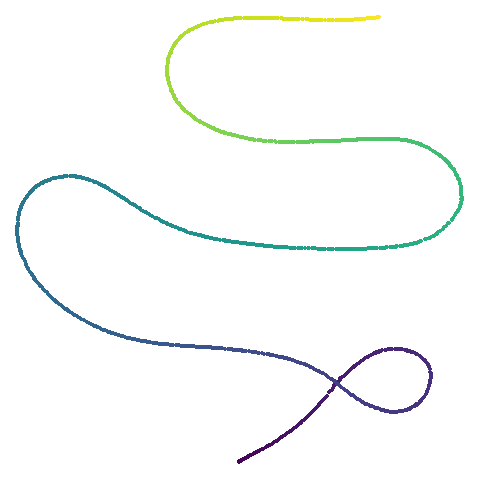mammoth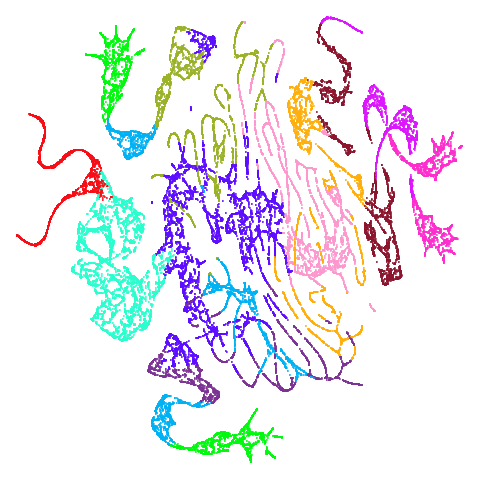
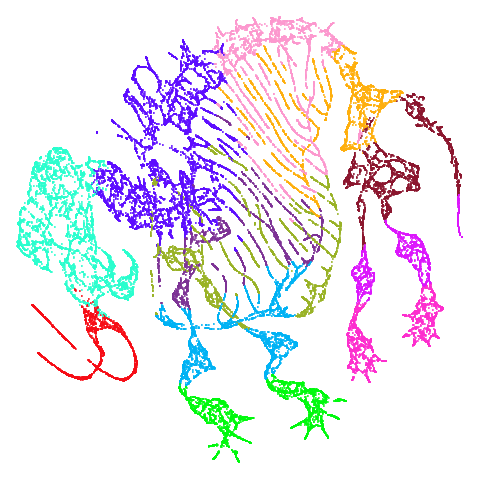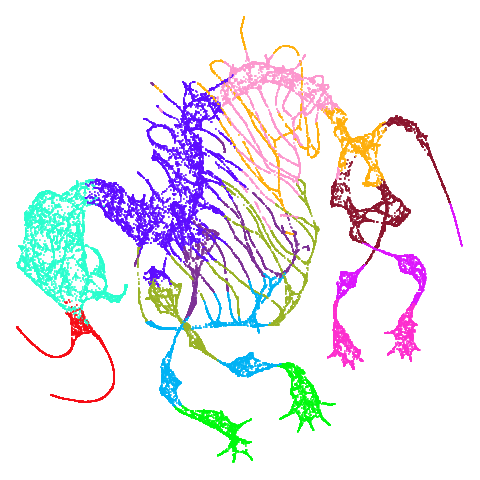scurvehole
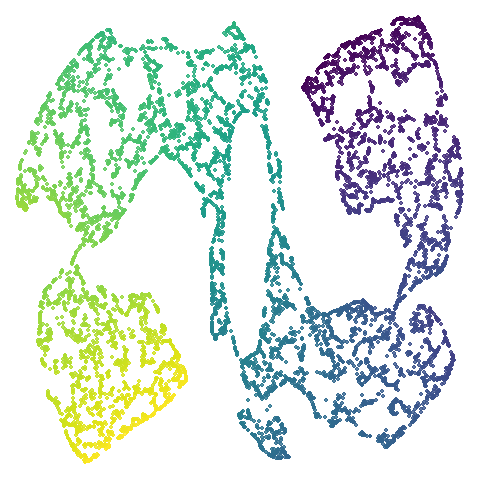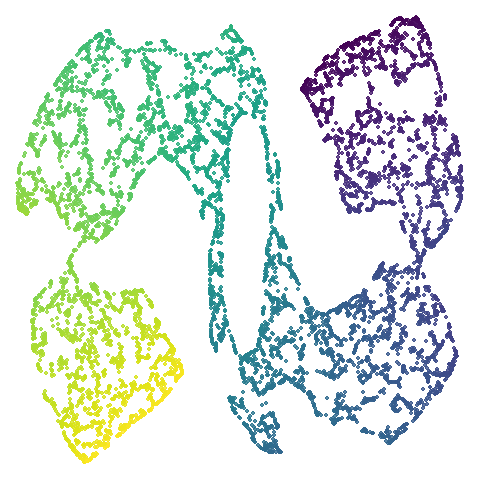isoswiss
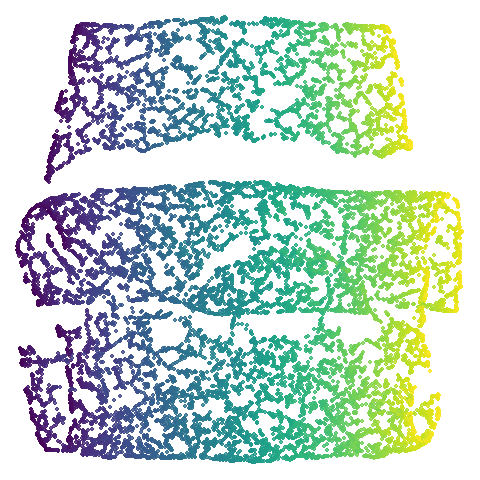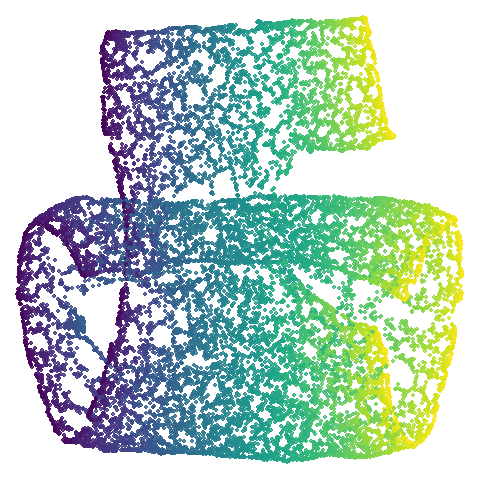hierarchical
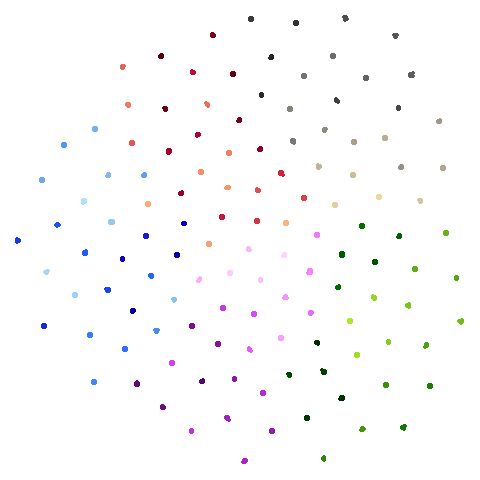spheres
coil20
coil100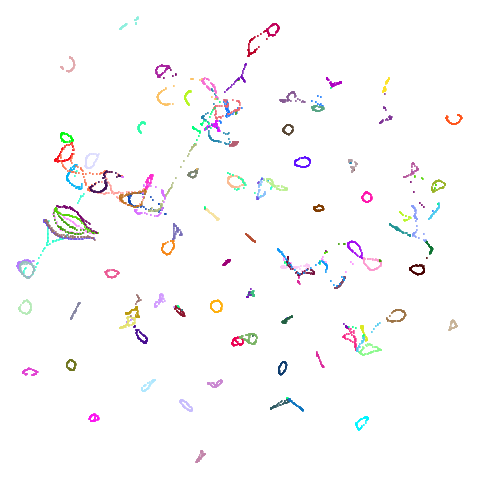
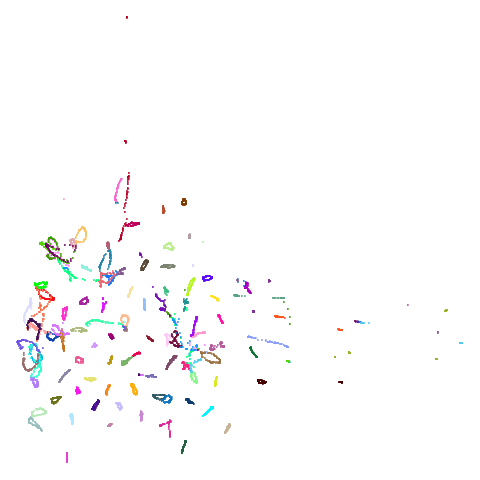macosko2015
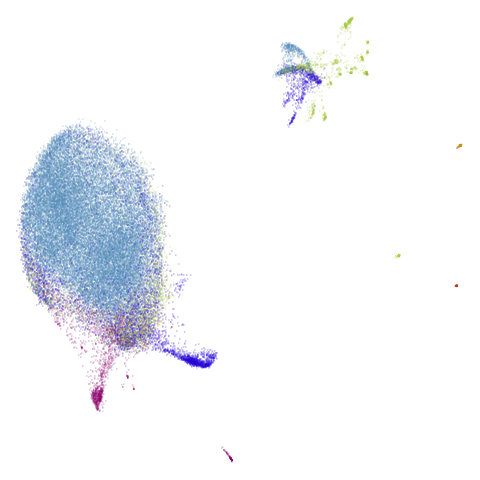mnist
fashion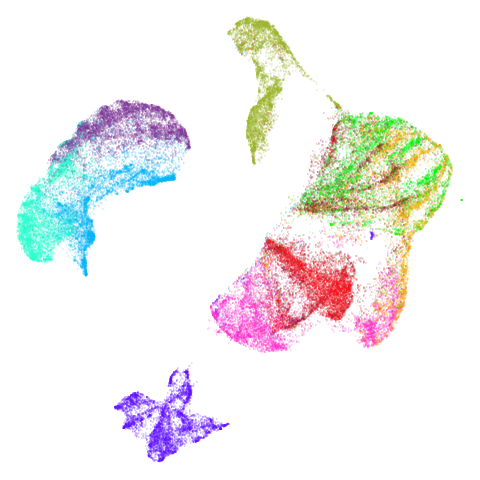
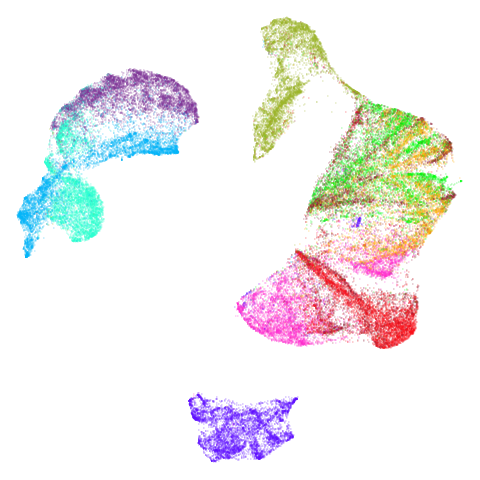ng20pacmap

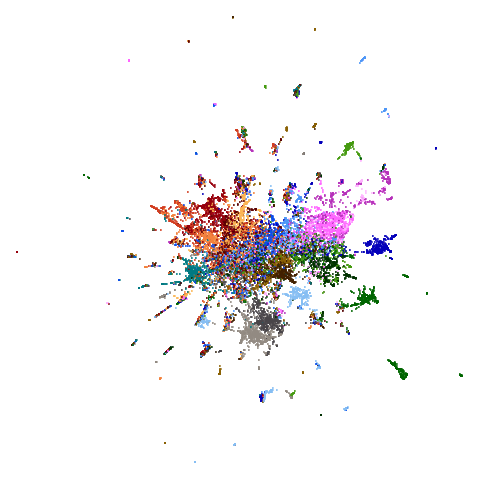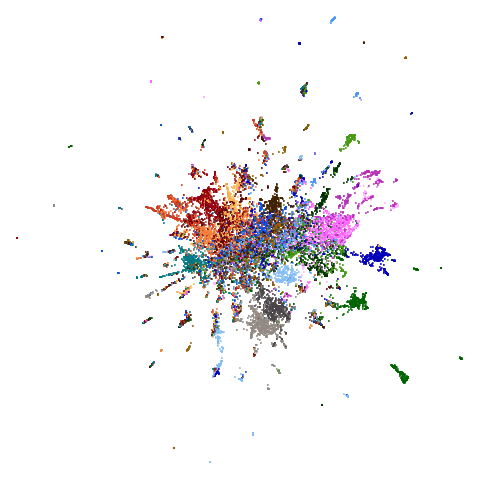Headline results from my point of view are that going from left to right, UMAP results get more like PaCMAP. But in many cases the default UMAP results don’t seem that different to the PaCMAP results. In a lot of these datasets, where there are differences, they have already been discussed at length in the PaCMAP paper, but in act of enormous ego I will provide my own commentary, you lucky things.

UMAP certainly makescurve2d a lot twistier than PaCMAP. And mammoth looks very different. It’s been brutally spatchcocked by UMAP, but it’s not been ripped to shreds. However, it’s undeniable that the human eye definitely perceives the side-on view that PaCMAP provides as being more “natural”. Also scurvehole demonstrates that UMAP has a tendency to rip low-dimensional manifolds more than PaCMAP. That said this dataset does often get ripped by PaCMAP too (both the ends and – less often – the area around the hold can be ripped), although the degree of ripping is not as pronounced as for UMAP.

Let’s also look at isoswiss. Here UMAP is better than PaCMAP and does a good job at nearly unfolding it. It’s a bit hard to see what PaCMAP has done here, but it’s undone by the PCA initialization which keeps the data rolled up. There has been some unrolling, but it’s tough to ask a method that works on iteratively updating pairs of points to do the large scale rearrangement of unfolding, and instead the top part of the embedding has been ripped.

You can see the same thing happening to a lesser extent with scurvehole where the two ends are a bit twisted. This is the same issue with a PCA initialization not being local enough. Is it the end of the world? No. It’s just a bit of a shame we have to sacrifice unfolding of these manifold examples given that the “M” in PaCMAP also stands for “manifold”.

But these are all low-dimensional datasets. I would love to see methods that could adapt to the intrinsic dimensionality of the data they are working on, and PaCMAP’s gentler approach is definitely superior here. But I am not sure that these are representative of the kind of data that people are actually working with. And whether there are lots of nice low-dimensional manifolds out there waiting to be unfolded is an open question. If not, then PCA is a good enough initialization for most datasets.

I’ll also briefly note something a bit odd about spheres. Neither UMAP nor PaCMAP do a good job at recognizing that the ten clusters are embedded in a larger sphere. Perhaps not surprising due to the local nature of these methods. But while UMAP gives a result with ten clusters, representing the ten spheres, plus the points from the other cluster that were most local to them, PaCMAP has eleven clusters. There is a large blob off to the side that seems to be just the background cluster. Interesting, and maybe you might like this result better due to it detecting the other sphere, even if the “containment” relationship hasn’t been preserved. However, I have seen artifactual behavior with Annoy sometimes when there are lots of degenerate distances and the parameters haven’t been set correctly. So there is a possibility that this is an artifact of the nearest neighbor method having some issues. That would be something to rule out but I haven’t done that here.

coil100 is an interesting case and is why I think the “multiply the PCA coordinates by 0.01” approach of PaCMAP may give slightly inconsistent initialization on occasion. UMAP gives a circular-looking result, whereas PaCMAP is more elongated, with some of the circular structures noticeably above or to the right of the body of the embedding. This is a case where the PaCMAP result is very influenced by the PCA initialization: the overall extent of the initialization is quite a large value: the side length of the bounding box of the initialized coordinates is around ~200 units vs ~30 for the PCA initialization of mnist. This leads to large interpoint distances which is the enemy of all SNE-like methods: the gradients are smaller than usual and hence more of the initial structure is kept. This could be seen as a good thing, because you might want to keep more of the PCA-inspired layout and focus more on local optimization. However, it’s not something that happens consistently with PaCMAP, it really depends on the initial scaling of the input dataset. Having a better scaling of the input coordinates would help here, such as the UMAP approach of scaling the coordinates to a cube of length 10.

Of the other datasets, the one that stands out as most different between UMAP and PaCMAP to my eyes is macosko2015. The PaCMAP result looks much nicer here. I like this dataset because results are very affected by PCA.

Now let’s see what using PCA initialization does to UMAP. The obvious place to look is at mammoth and here we see that the results are now much closer to PaCMAP’s. The same is true for curve2d and isoswiss. scurvehole also has an overall layout much closer to PaCMAP, but the degree of twisting and ripping is definitely worse for UMAP.

Elsewhere, things aren’t changed so much. I admit I am a bit annoyed by the result for coil20 where one ring on the left is now stuck inside a larger ring which isn’t the case for the spectral initialization of PaCMAP but I will get over it. The UMAP + PCA result for coil100 also has the same circular shape as with the spectral initialization rather than the elongated shape of the PaCMAP result which I argue is further evidence that more control over the initial scaling of PaCMAP could be helpful.

I also would say that in terms of overall layout, whether the mnist cluster layout for UMAP or UMAP+PCA is more like the PaCMAP result is a bit of a toss-up. But how well these methods work on mnist is the last thing anyone should worry about. That really leaves macosko2015 whch still bears little resemblance to the PaCMAP result.

In the third column we use PCA to reduce the initial dimensionality of the data to 100 and we use the first two principal components as the initial coordinates. This will only give a difference in results compared to the UMAP+PCA results if the input data has more than 100 columns, which is not the case for most of the datasets at the top of the table. Further down not much happens except for macosko2015, which now looks much more like the PaCMAP results. This was not terribly surprising to me because I know that this dataset is highly affected by running PCA on it first.

Conclusions

If you want a more PaCMAP-like experience out of uwot using pca = 100, init = "pca" is a good way to go. Even for lower-dimensional synthetic data, PCA will give you results closer to PaCMAP, although they may look a bit more raggedy.

What about random initialization?

One of PaCMAP’s selling points is that you will get more consistent results even if you don’t use PCA for initialization. I will grant you that this is certainly a point in PaCMAP’s favor. But on the other hand, there’s a limited number of circumstances where you can’t just use PCA for initialization. The PaCMAP paper doesn’t go into detail about what these circumstances are, so I will just give you some of my ideas. The main one might be that you have data which doesn’t really lend itself to PCA. Probably binary data is the most obvious case here, although PaCMAP only supports the Hamming distance for binary data so your options are a bit limited anyway. Another example might be where the data is such that you have access to the k-nearest neighbors but not the underlying ambient data. But in that case, you would not be able to generate the mid-near pairs needed for PaCMAP’s performance so you would be out of luck anyway.

However, I am sure other scenarios exist. In those cases, PaCMAP is a good choice. For other cases we can make UMAP do what we want in uwot easily enough.

Ok, but will it be as fast?

The bottleneck for most of these methods is the speed of the nearest neighbor search which is in turn dependent on the input dimensionality. So if the PCA process is sufficiently fast then the overall speed of the PaCMAP approach will outperform the UMAP approach. In uwot I find that irlba tends to be a bit slower than the truncated SVD available in sklearn in Python as used by PaCMAP but it depends on the linear algebra library on your system.

Due to some other internal differences, I would still anticipate that PaCMAP will be a bit faster than UMAP under these conditions. In practice, the difference isn’t that large in my experience (a few seconds for mnist, for example). If speed matters to you then I recommend using:

a = 1, b = 1 with umap2 if you don’t mind a t-UMAP-like appearance.
Or use approx_pow = TRUE if you do want to control min_dist and spread (or a and b directly).
negative_sample_rate = 4 will reduce the amount of negative sampling in line with what PaCMAP effectively does and shouldn’t affect things too much.
consider using rng_type = "deterministic", which will not use a random number generator at all for the negative sampling. If you want pseudo-random sampling, then rng_type = "tausworthe" is faster than the default.

On the other hand, if speed really matters, then PaCMAP will give you vital seconds back without having to fiddle with the UMAP defaults.

Making UMAP behave (more) like PaCMAP