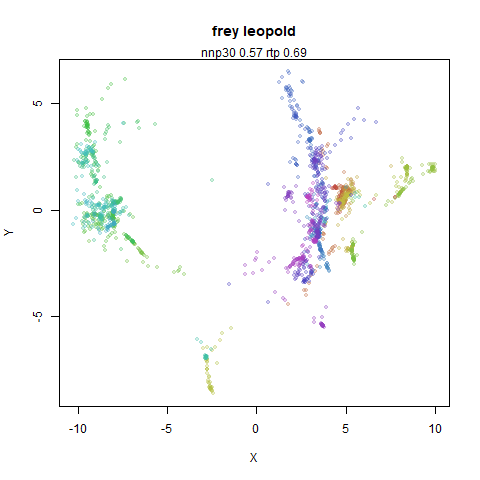
Leopold: Lightweight Estimate of Preservation of Local Density

Approximating densMAP

February 16 2022

densMAP

densMAP is a variation on UMAP that attempts to preserve the differences in density in the original data by adding a new component to the cost function. It is available in the Python UMAP implementation by setting densmap=True. See also this excellent tutorial. There has been a request to add densMAP to uwot since the start of 2021. This document describes the approximate version of densMAP that is available in uwot which may be good enough. But first, a bit more about densMAP.

densMAP can be seen as adding a regularization to the UMAP cost function in which the “local radius” of each observation in the input and output space is calculated and the Pearson correlation between the two is optimized.

The radius of observation $i$, $R_i$ is calculated as:

$$R_i = \frac{1}{\sum_i P_{ij}} \sum_i d_{ij}^2 P_{ij}$$

where $d_{ij}$ is the distance between point $i$ and $j$ and $P_{ij}$ is the symmetrized edge weight between $i$ and $j$, i.e. the radius is the edge-weighted average of the squared distances between each $i$ and each of its neighbors. Because the matrix has been symmetrized, $i$ may have a different number of neighbors than the n_neighbors parameter that the user specifies.

To get a feel for what densMAP does, below are some results from the Python UMAP (i.e. no uwot output here), with and without densmap=True. As recommended by the current UMAP README, I also set n_neighbors=30, except for subset_clusters, which I’ll explain when I get to it. Everything else was left as the defaults.

The images below are:

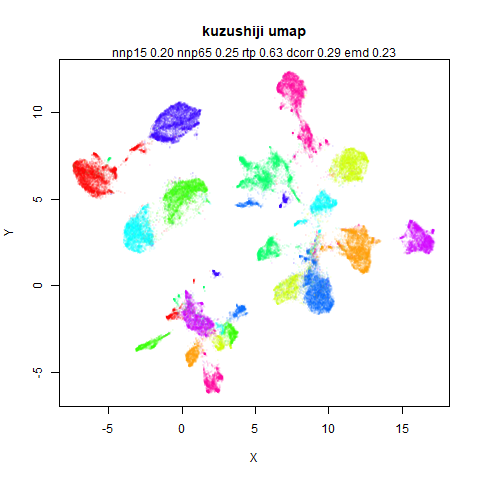
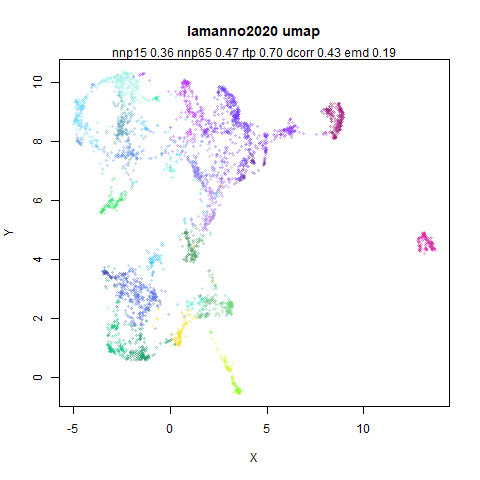
• Top left: the UMAP results colored by the typical label for that dataset. There are some cryptic numbers in the subtitle which you should feel free to ignore.
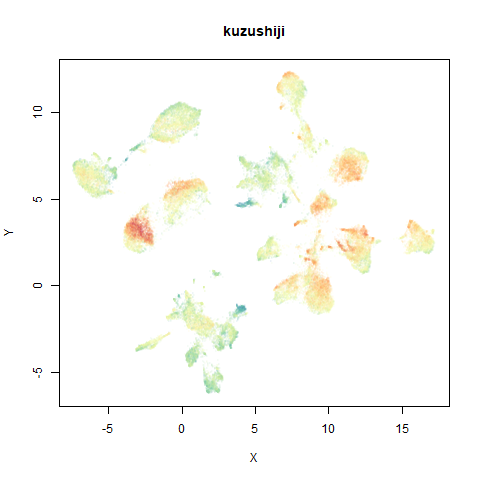
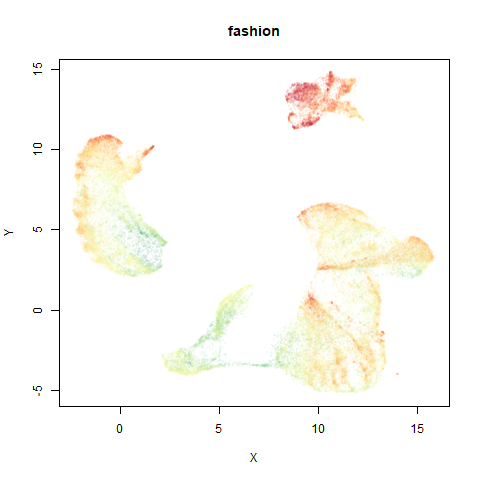
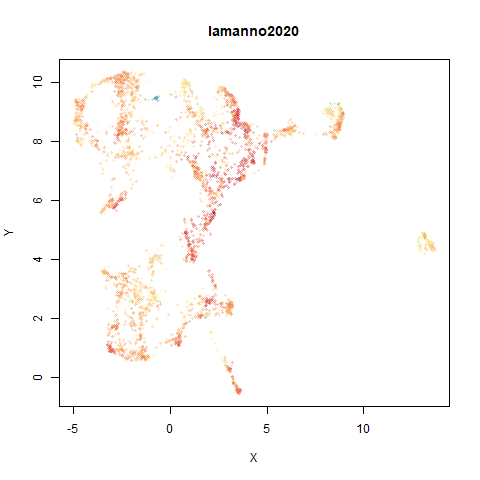
• Top right: UMAP results with each point colored by the log of the input local radius, using the ColorBrewer Spectral palette. Red means a small radius, blue means a large radius. This should show areas that densMAP is likely to contract or expand, respectively.
• Middle left: the densMAP results colored by the typical label for that dataset.
• Middle right: the densMAP results colored by local radius.
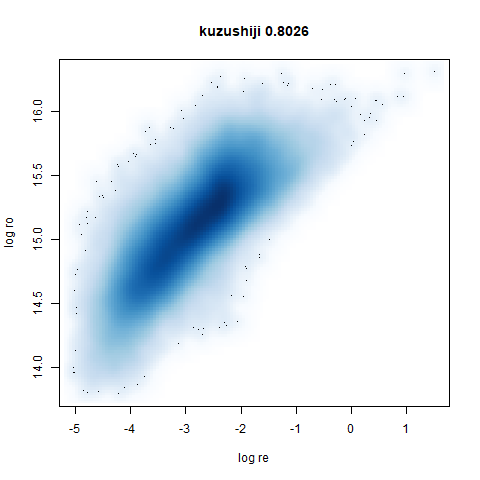
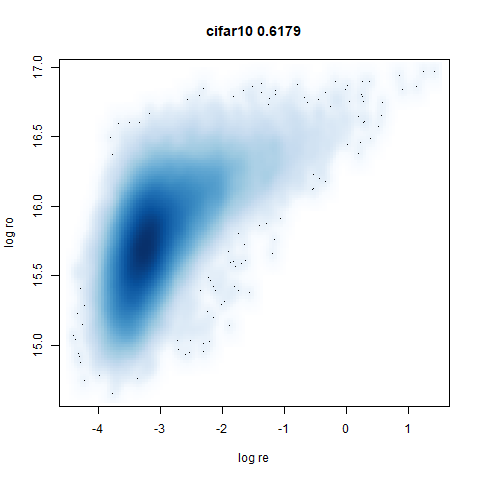
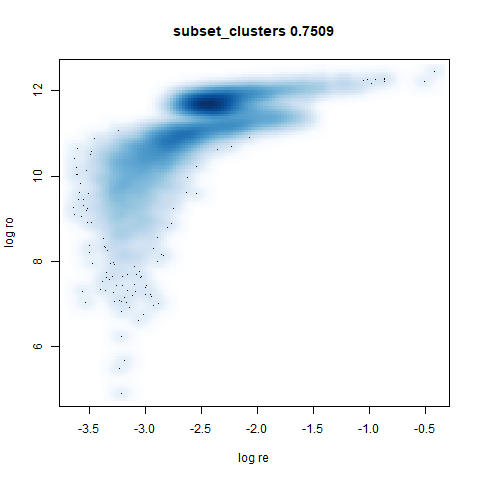
• Bottom: a plot of the log of the input local radii vs the log output radii and the Pearson correlation between them. These radii are returned from the fit_transform method when densmap=True. When there were more than 1000 points, I used smoothScatter to plot the results.

First two datasets are simple simulation sets based on How to Use t-SNE Effectively, specifically sections 2 (“Cluster sizes in a t-SNE plot mean nothing”) and 6 (“For topology, you may need more than one plot”).

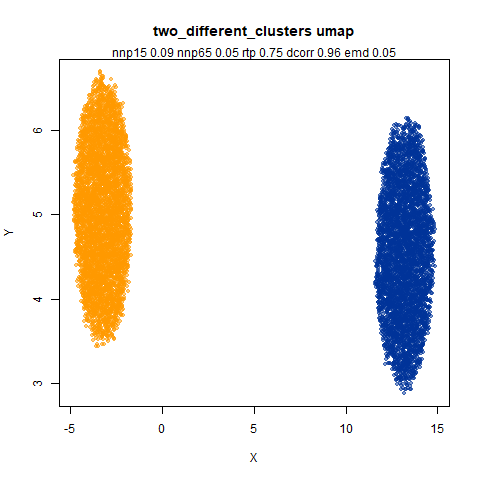
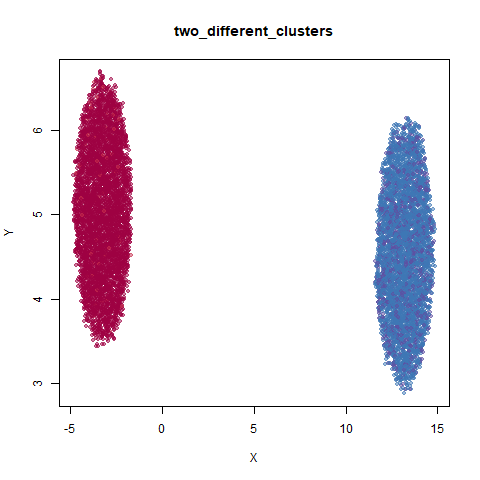
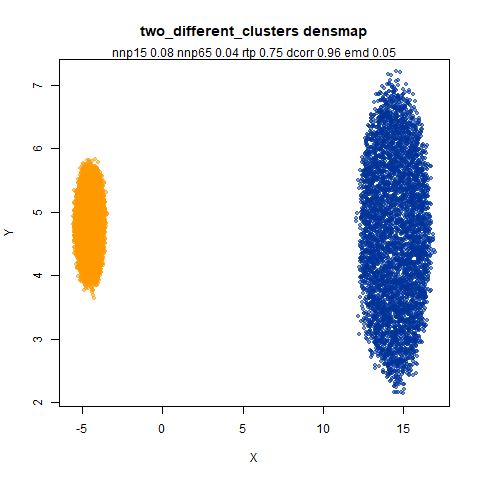
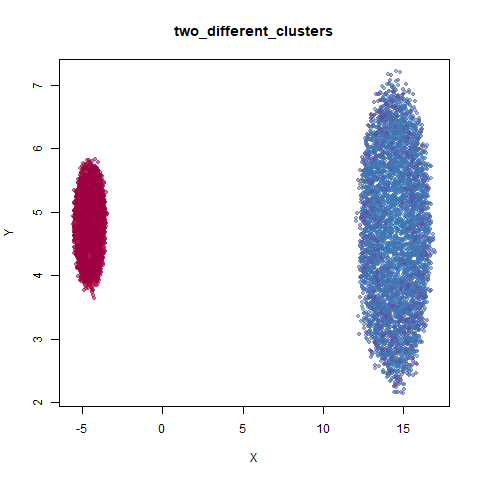
two_different_clusters

This dataset consists of two 50D Gaussians of 5,000 points each. One of the clusters has a standard deviation 10x the other. I used snedata to generate this data (via the two_different_clusters_data function).

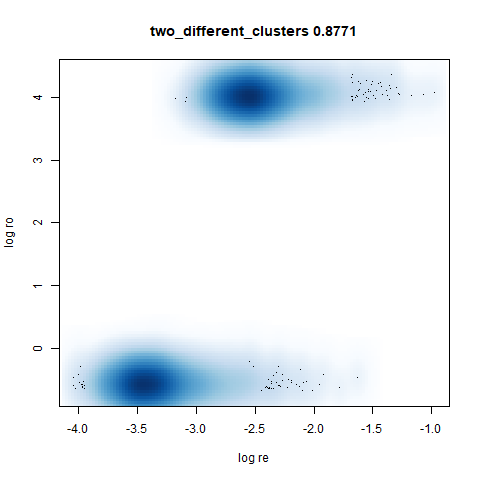Like t-SNE, default UMAP shows both of these clusters as the same size. densMAP shows one of the clusters as smaller. A good start.

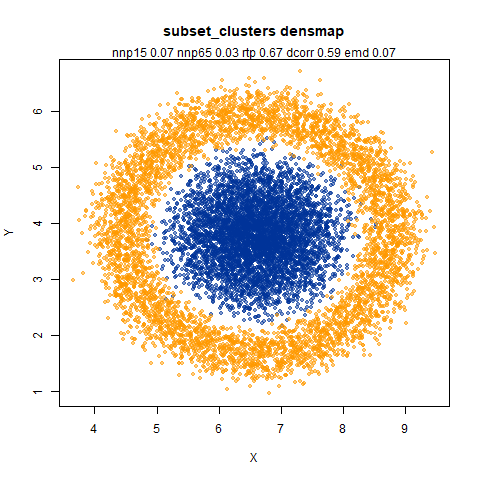
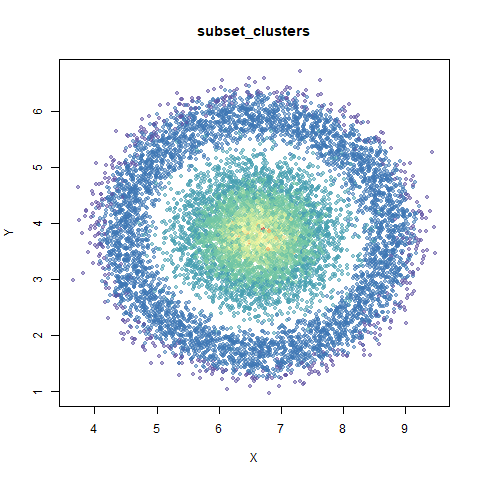
subset_clusters

This dataset once again features two 50D gaussians of 5,000 points each, but this time they overlap entirely. The larger cluster has a standard deviation of 50, the smaller a standard deviation of 1.

For this dataset I used n_neighbors=150, much larger than the n_neighbors=30 setting used for the other plots. This was to be consistent with the plots I generated with uwot. With uwot I precalculated exact nearest neighbors for all datasets and for this dataset, using the exact 30 nearest neighbors results in the smaller cluster being embedded at the edge of the larger cluster. Presumably 30 nearest neighbors doesn’t result in enough edges between the two clusters to properly situate the smaller cluster. The approximate nearest neighbors routine used in UMAP results in edges between sufficiently far away neighbors to create a neighborhood to that reflects the global structure better. I didn’t investigate this thoroughly, but it sounds plausible to me.

UMAP considers these two clusters to be the same size. With densMAP, the ring-shaped structure that is found with high perplexities with t-SNE shows up. But at least the small cluster is inside the big one. Note that if you re-run this with n_neighbors=30 the results are not noticeably changed.

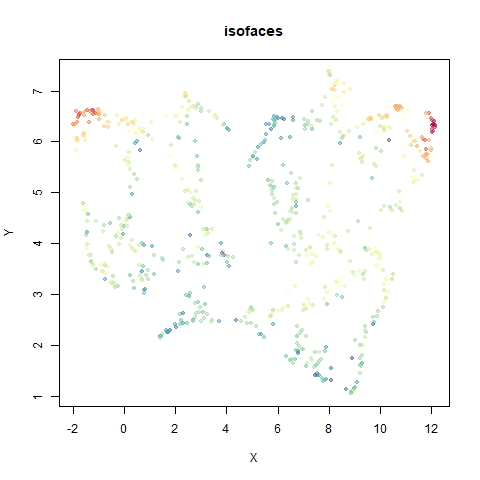
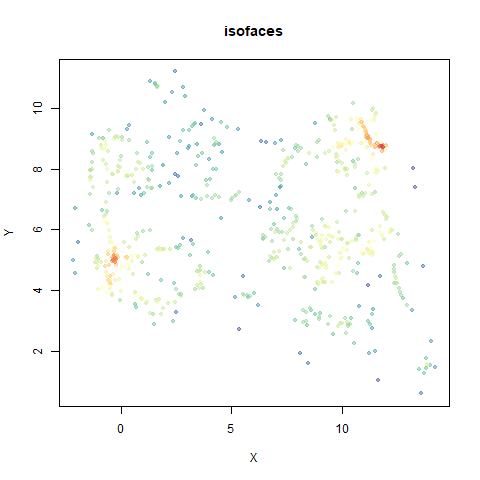
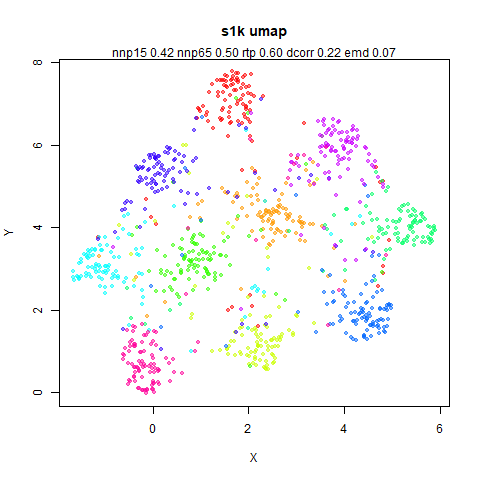
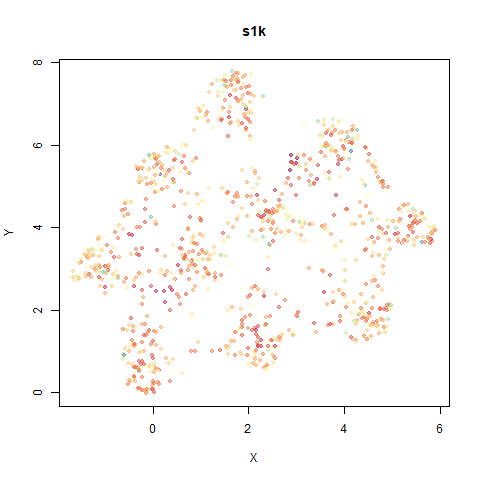
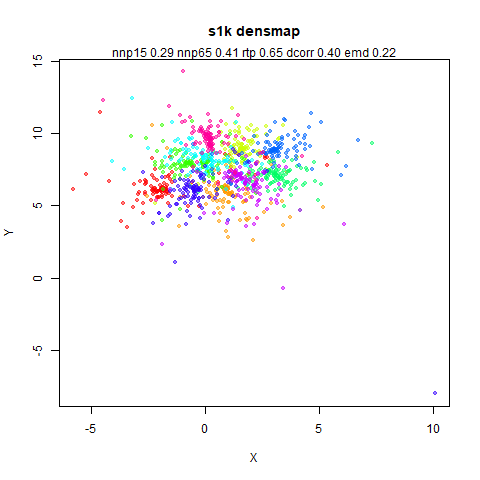
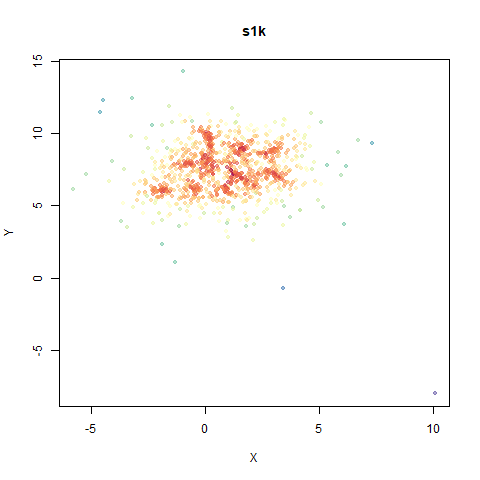
s1k

This is a synthetic dataset I like to use: 1000 points from a fuzzy 10D simplex.

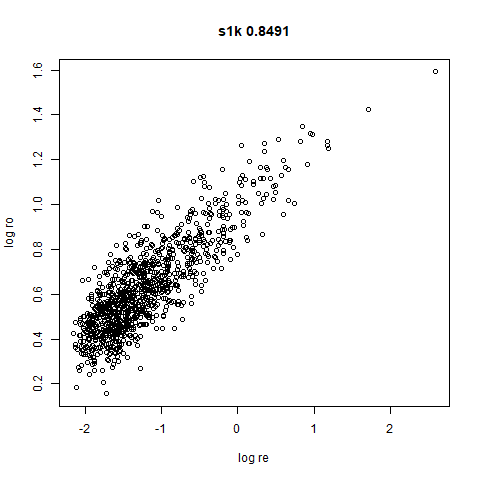I can’t say I like what densMAP has done here. There is one point that has been flung far away from the rest of the plot. You can see from the coloring that this is because it has a large local radius. This perhaps indicates that the local radius calculation can be affected by edge effects.

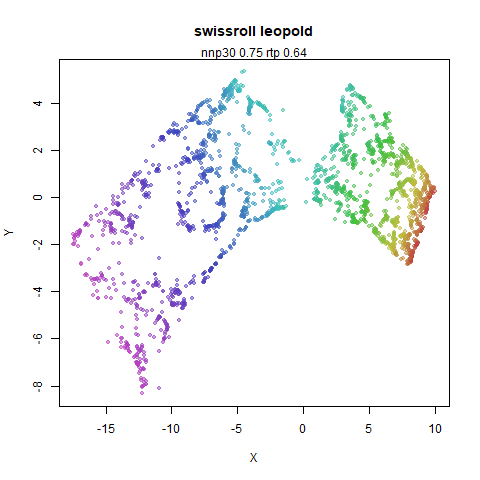
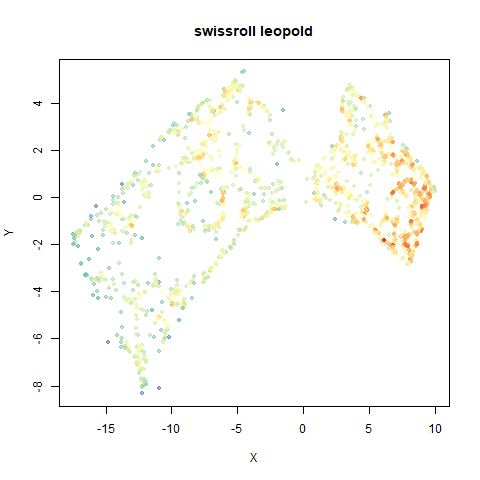
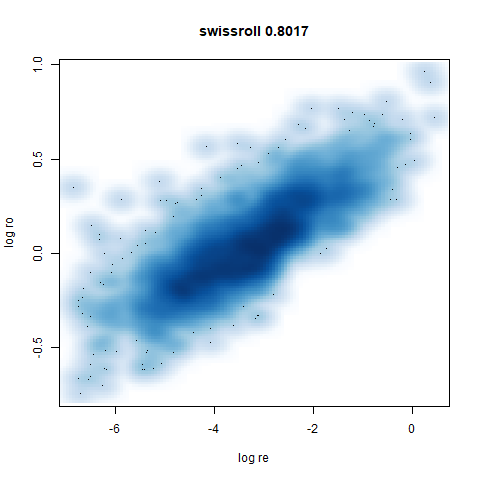
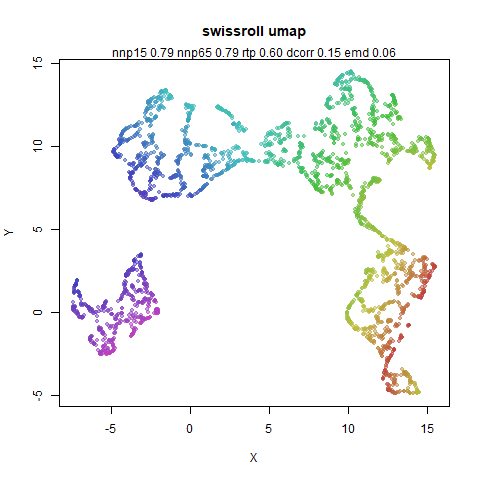
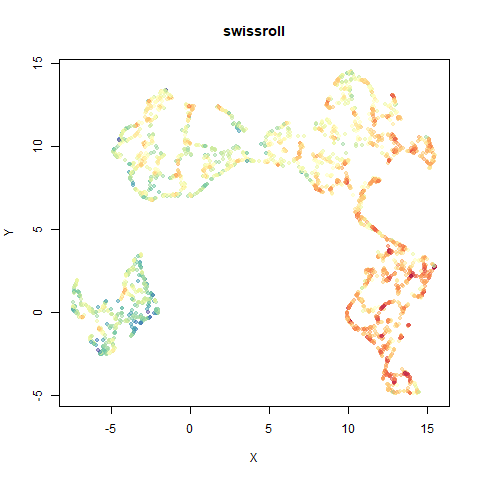
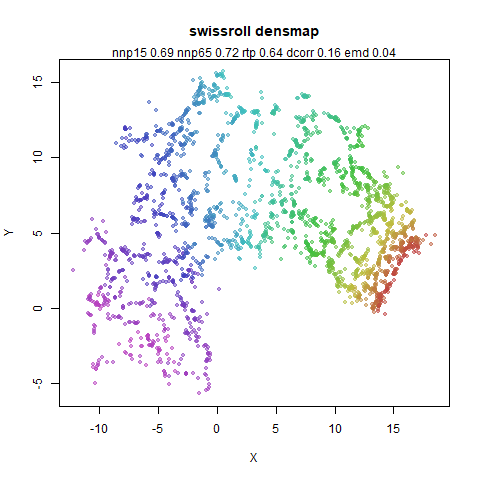
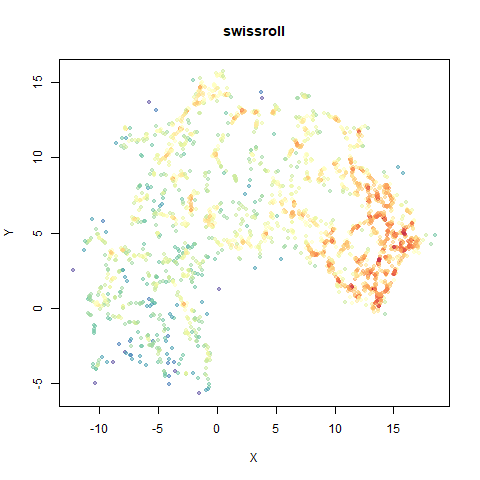
swissroll

A swiss roll dataset of my own devising.

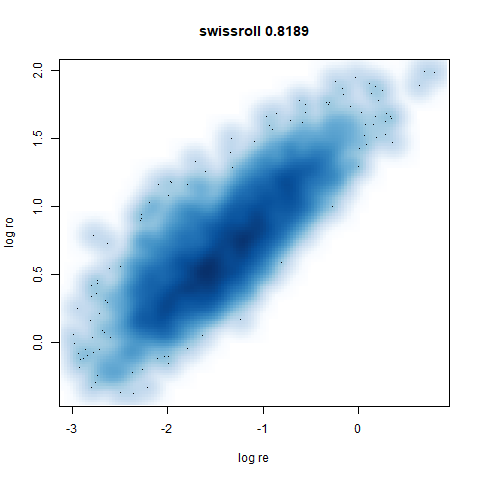densMAP does a noticeably better job at not ripping the swiss roll than UMAP does. As you would expect the local density to be fairly uniform across a 2D manifold I don’t know if there’s an a priori reason to have thought densMAP would do a better job here.

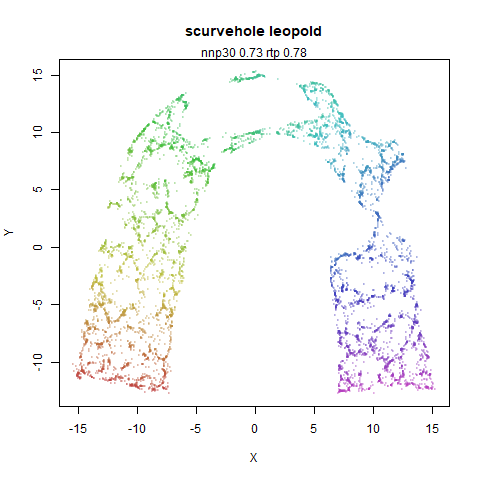
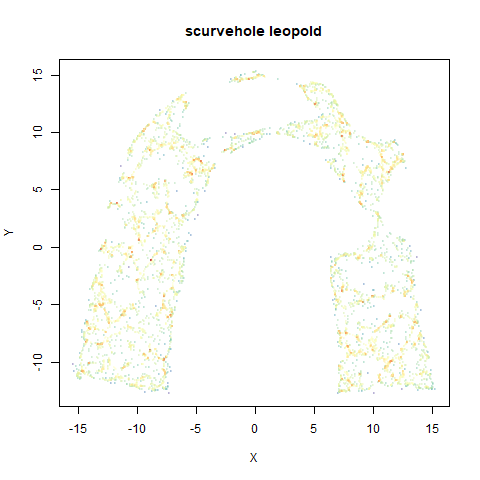
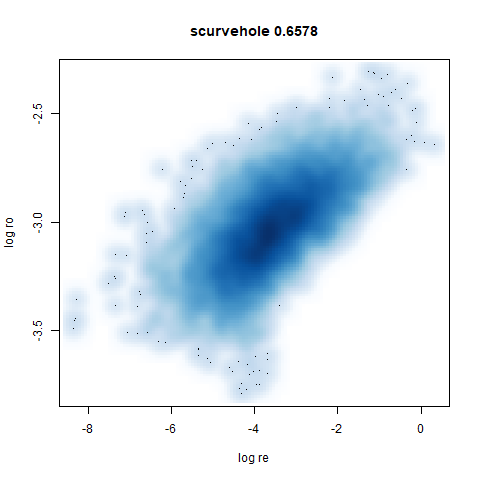
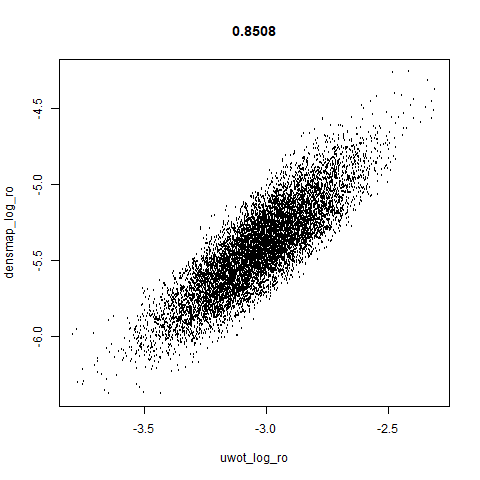
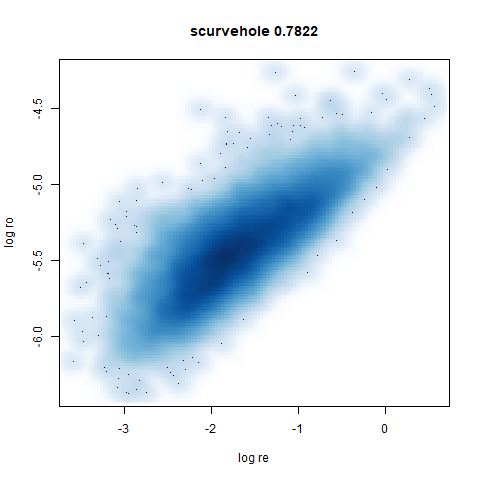
scurvehole

A 3D S-curve with a hole data set, used to validate the PaCMAP method (see also the github repo).

iris

Ronald Fisher’s iris dataset.

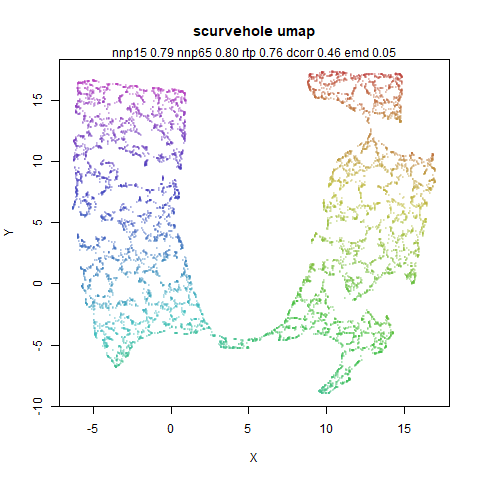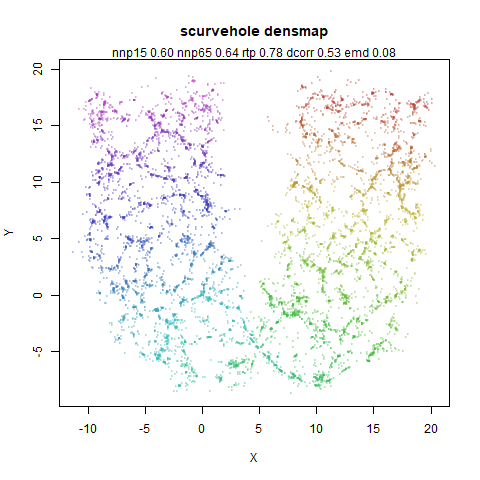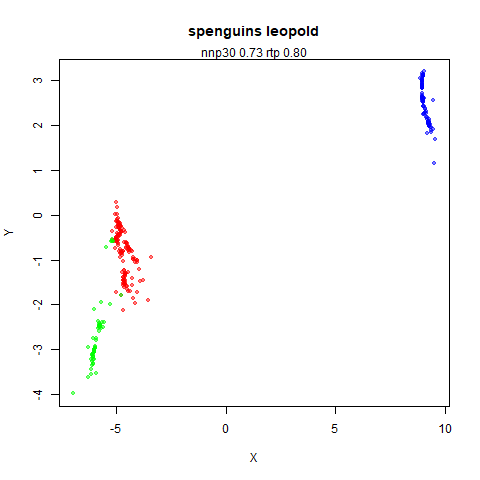
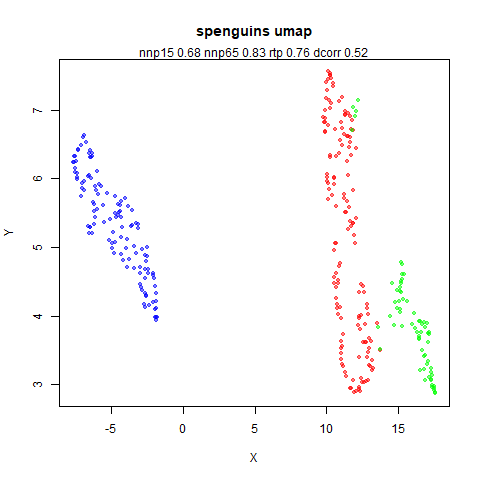
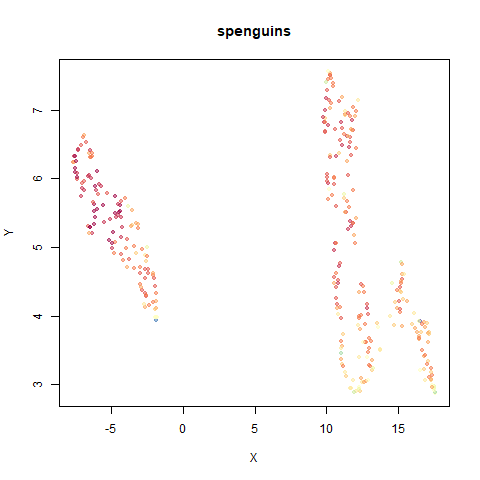
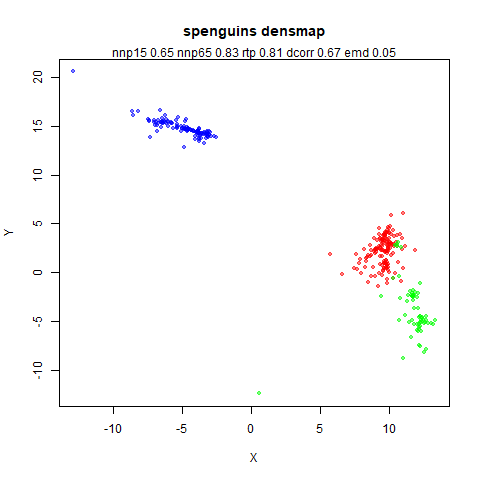
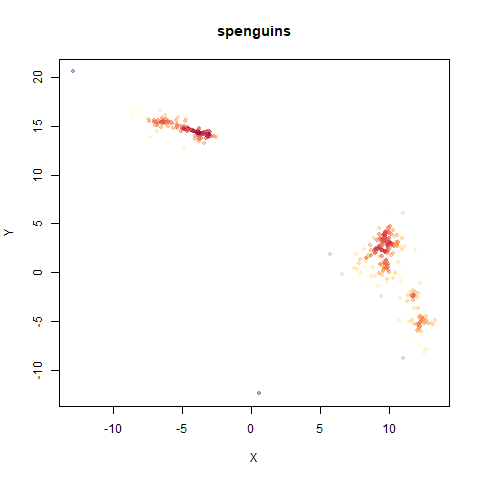
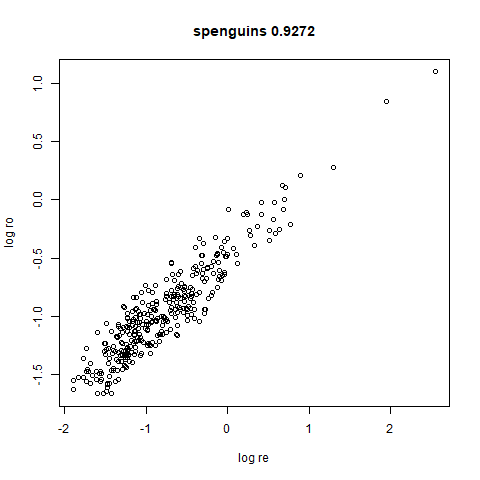
spenguins

The Palmer Penguins. The s in spenguins stands for scaled, because I filtered out entries with missing values then Z-scaled the inputs.

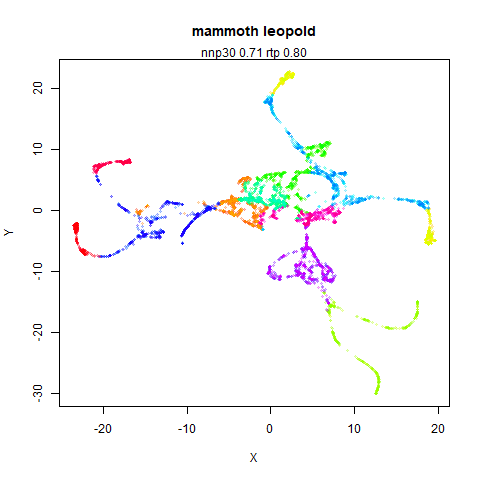
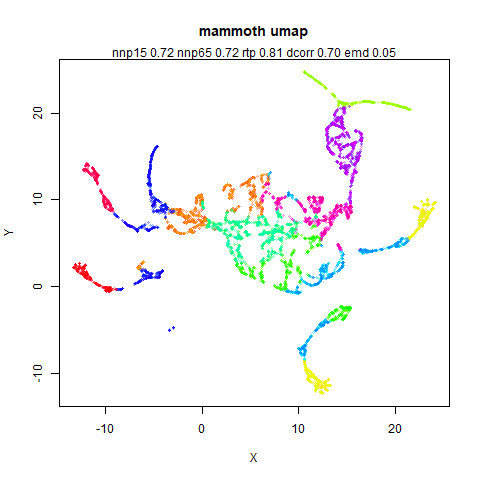
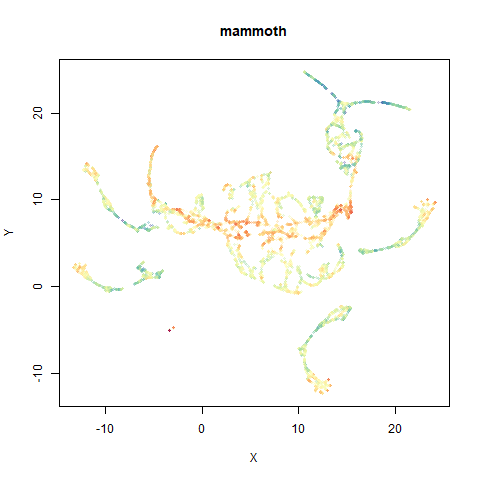
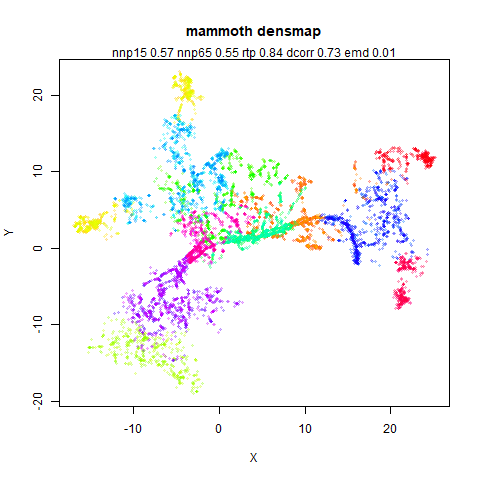
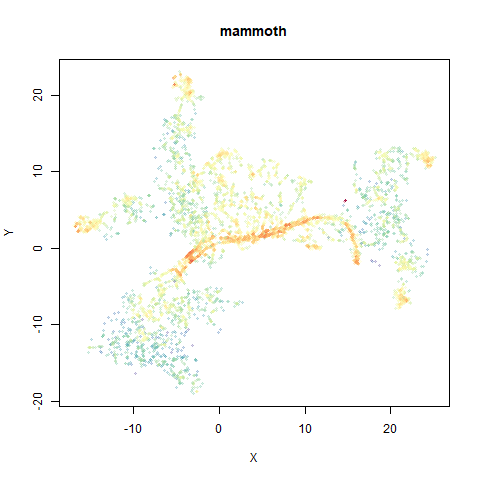
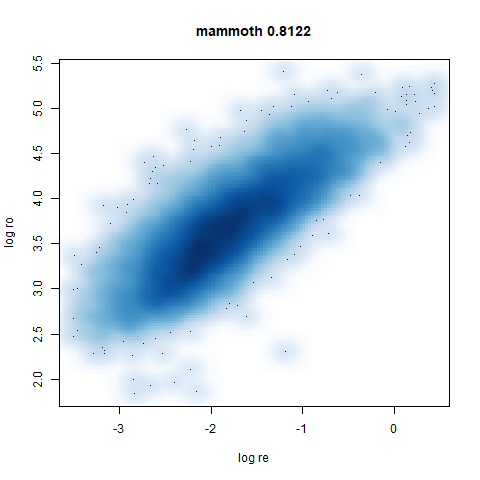
mammoth

A 3D point cloud of a mammoth at the Smithsonian, from Understanding UMAP, based on work originally done by Max Noichl.

oli

The Olivetti Faces images.

frey

The Frey Faces images.

isofaces

The faces dataset used in Isomap (processed via this gist).

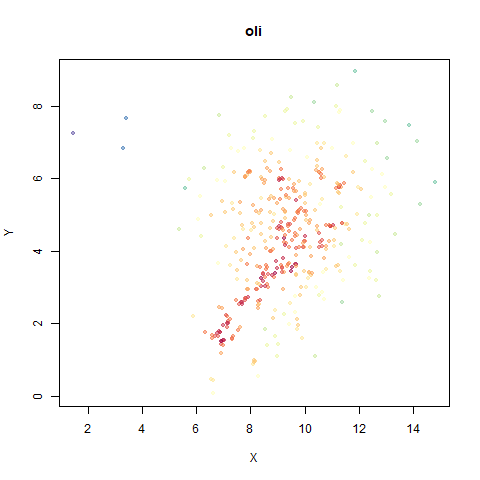
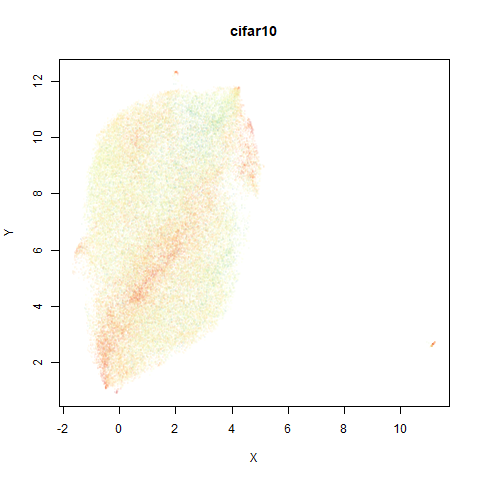
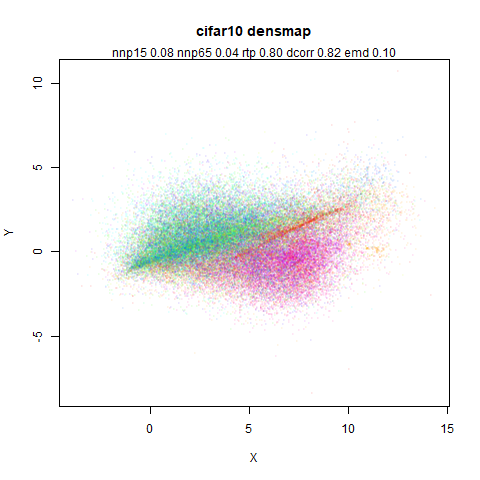
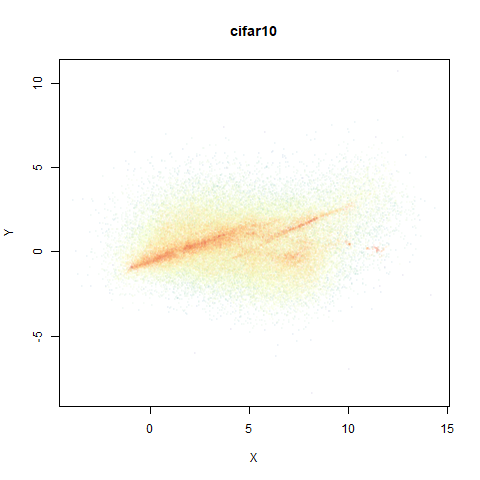
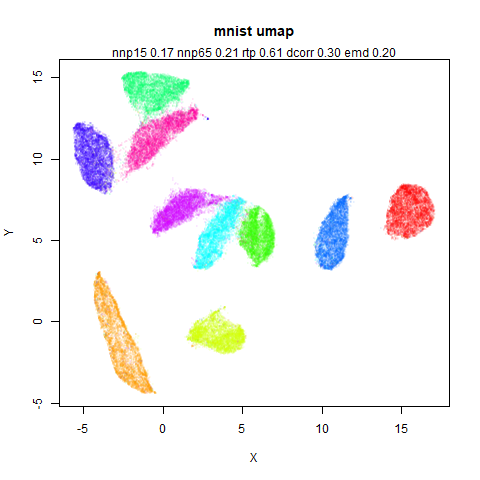
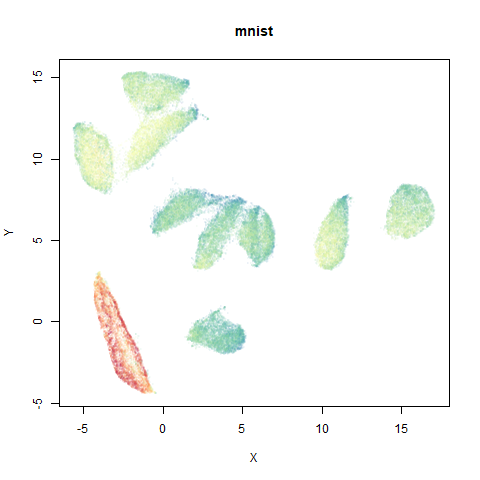
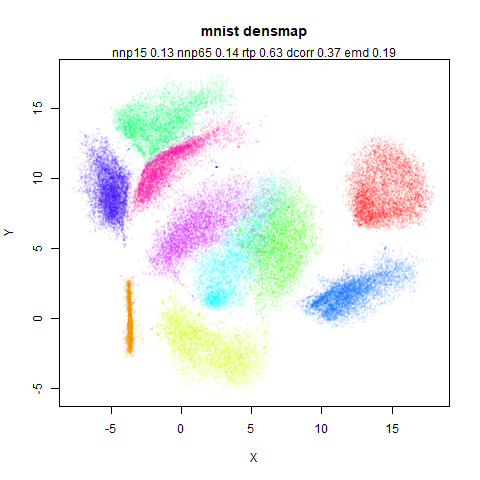
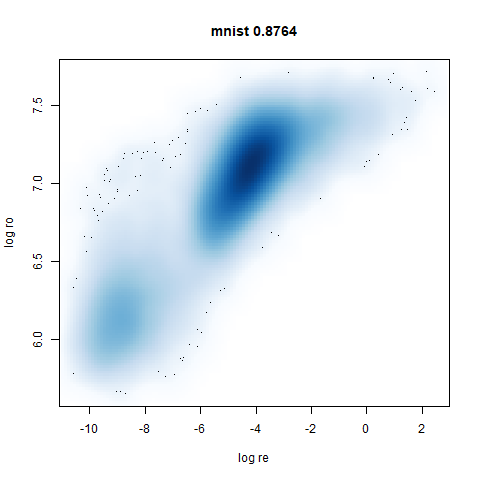
mnist

The MNIST digits images.

The orange cluster is the 1 digits and its smaller radius is exceptionally obvious when coloring the UMAP plot by radius. It very noticeably shrinks when densMAP goes to work on it.

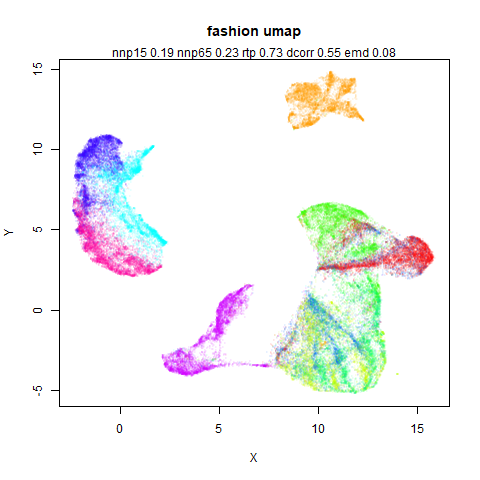
fashion

The Fashion MNIST images.

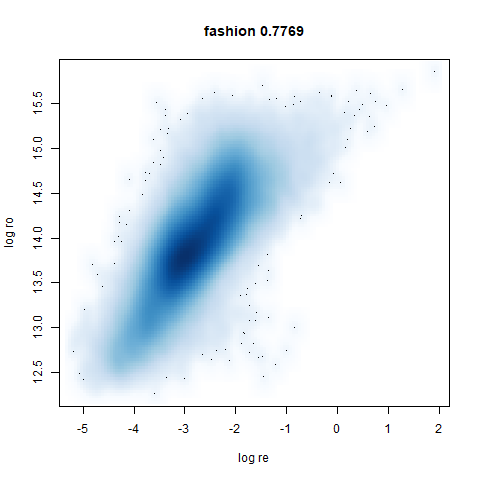Similarly to the MNIST digits, the orange cluster (this time its images of pants) is noticeably smaller than the other clusters.

kuzushiji

The Kuzushiji MNIST images.

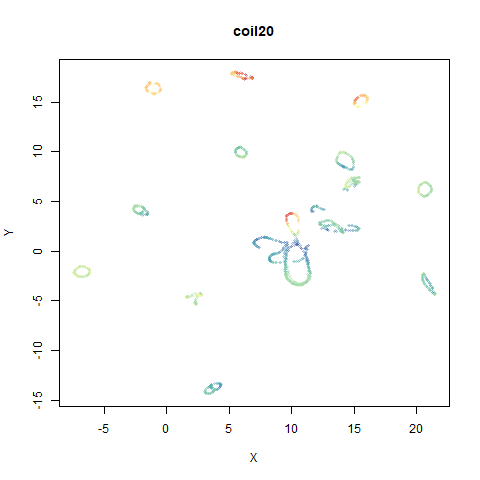
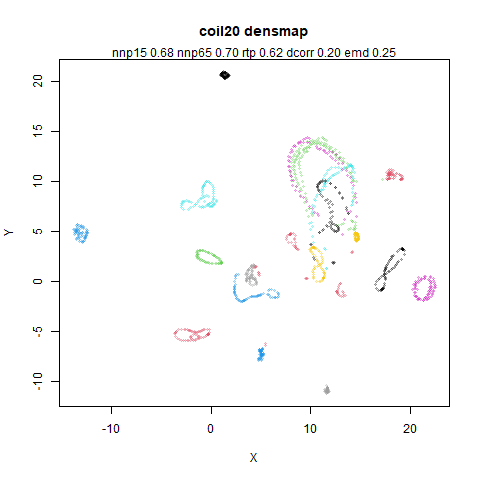
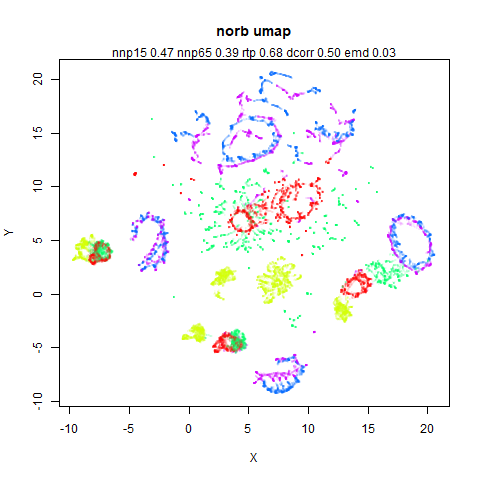
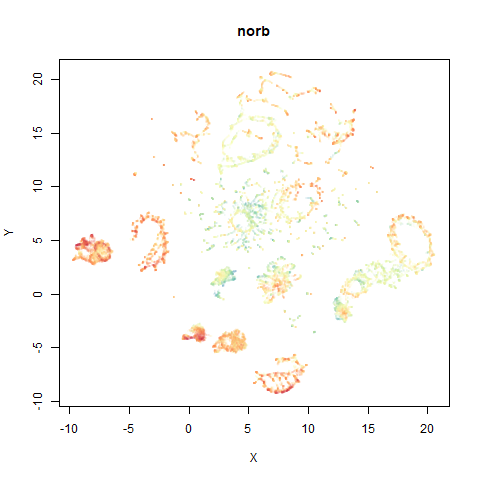
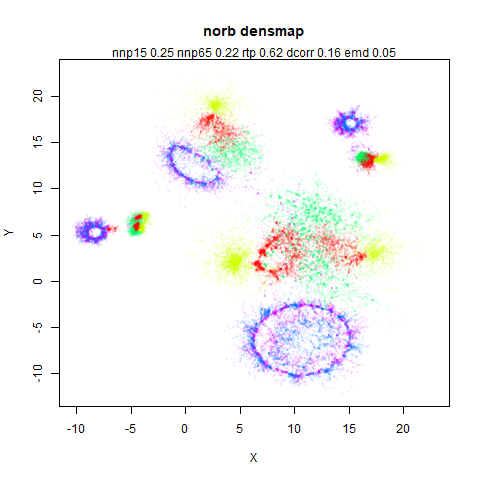
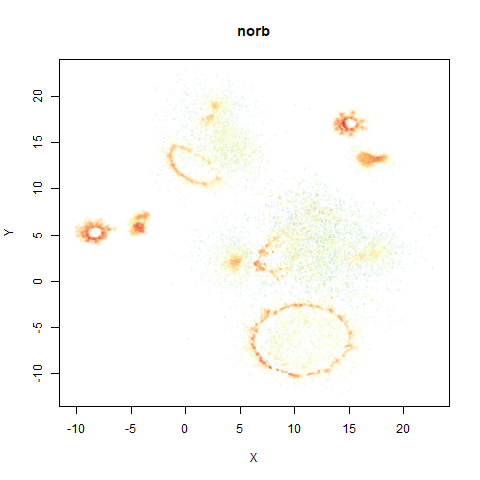
norb

The Small NORB images.

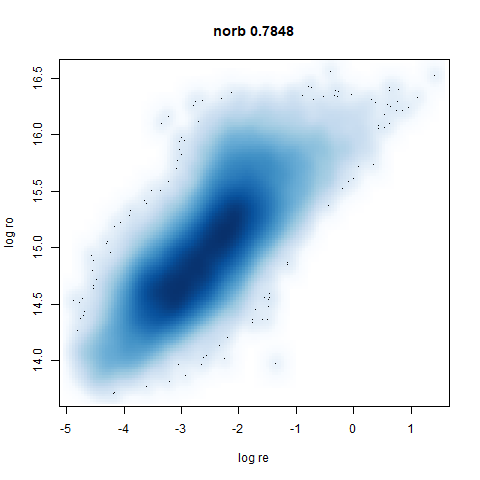You can see the largest of the blue/purple ring-like structures is broken up by UMAP, but densMAP preserves it. In fact, the densMAP plot is one of the nicer UMAP layouts of the small NORB datasets I’ve seen.

coil20

The COIL-20 images.

coil100

The COIL-100 images.

cifar10

The CIFAR-10 images.

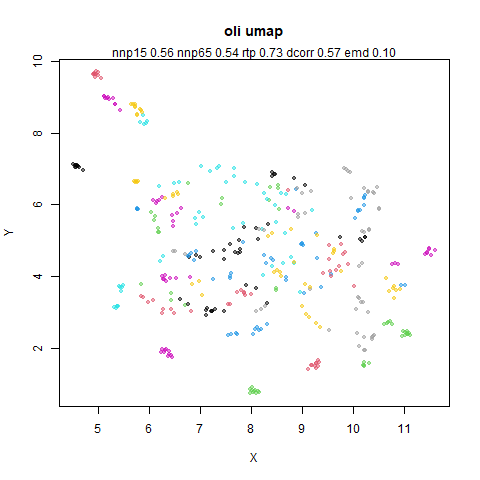
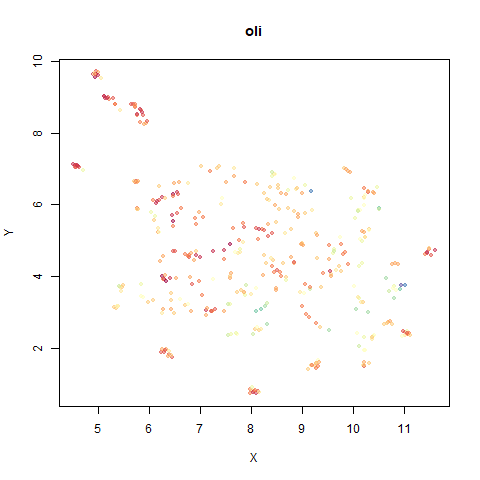
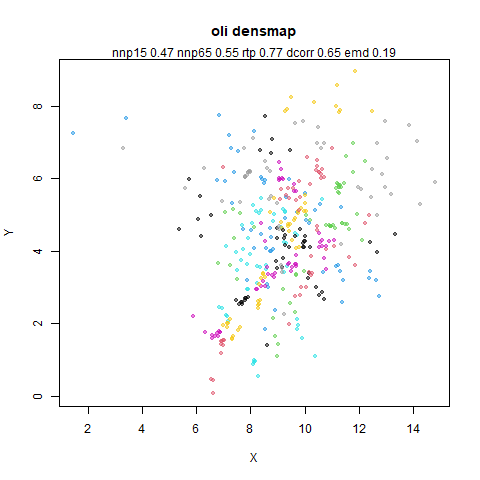
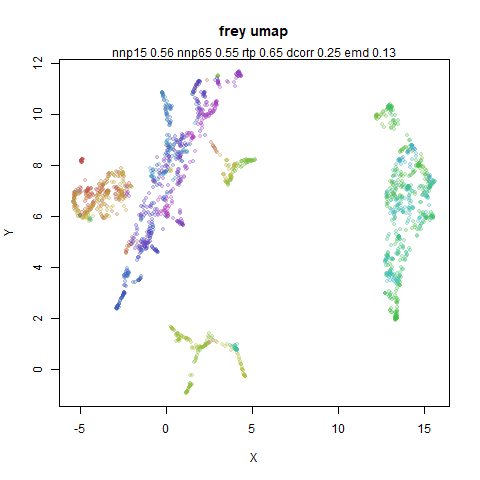
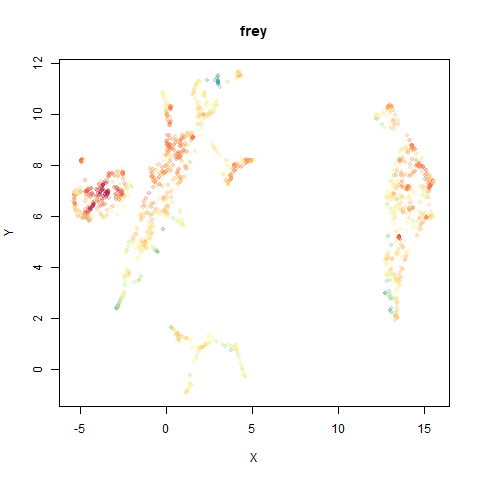
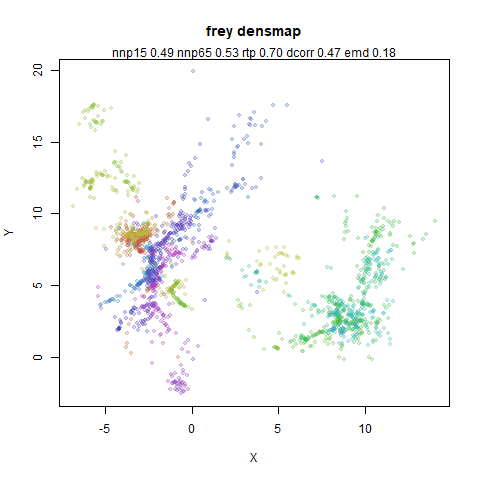
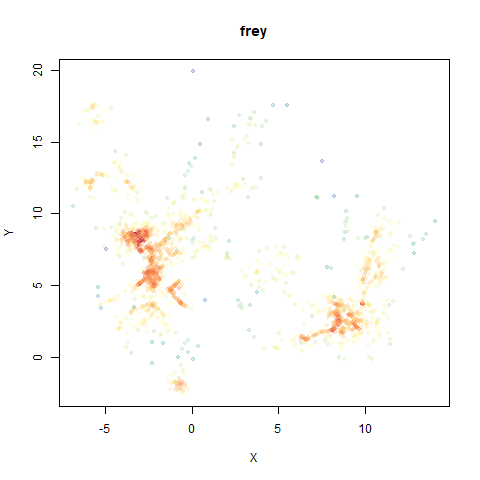
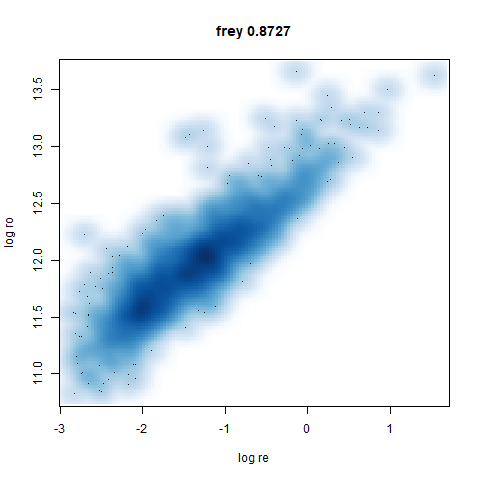
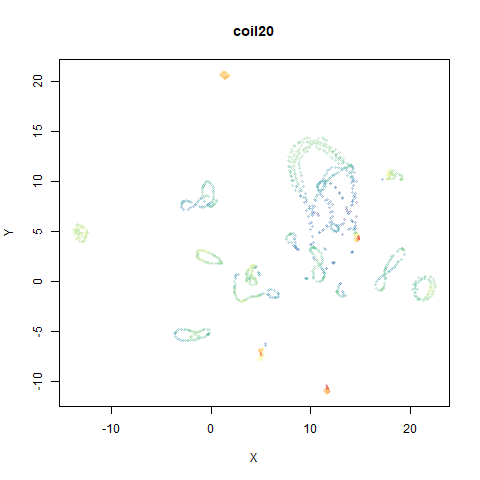
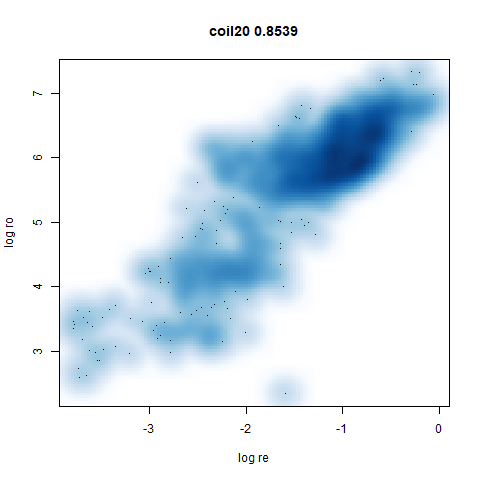
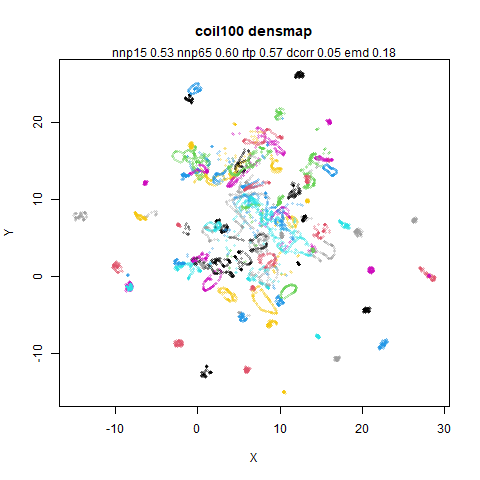
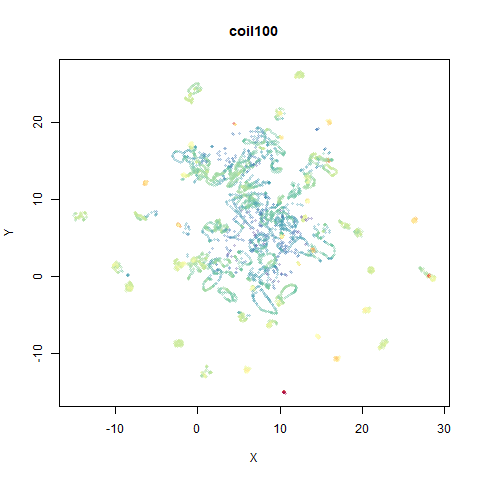
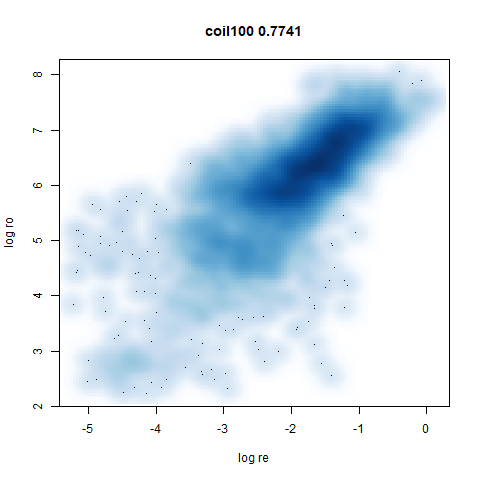
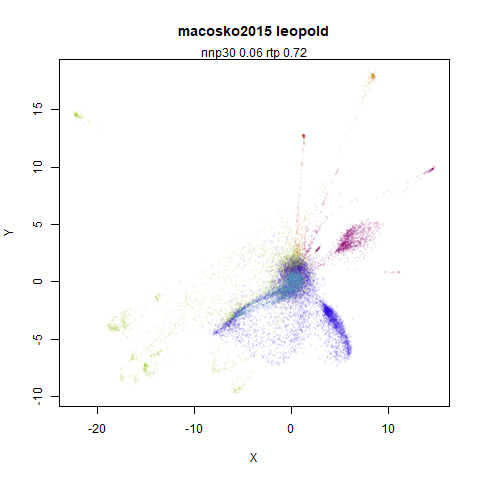
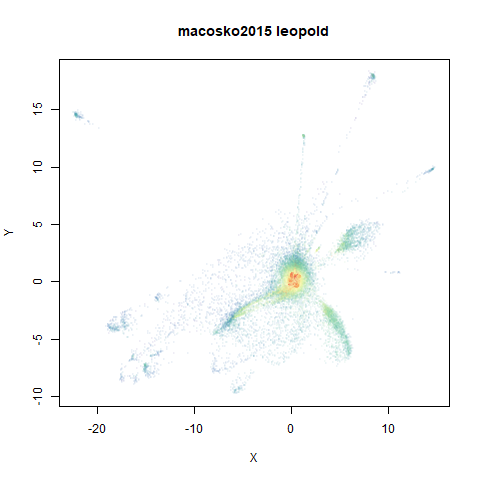
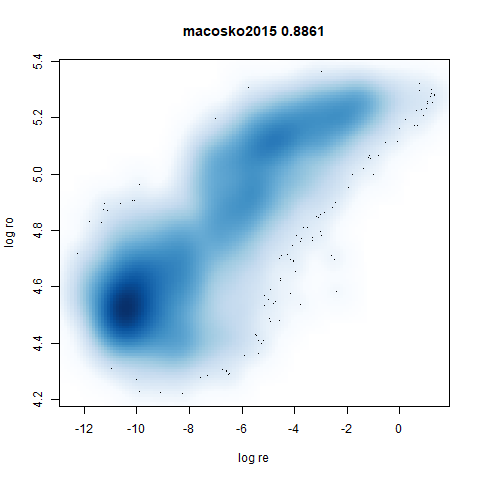
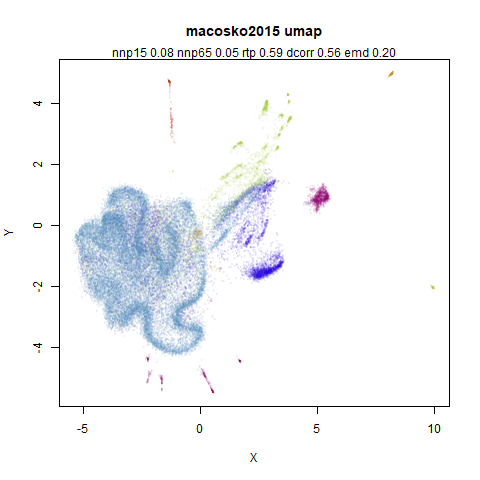
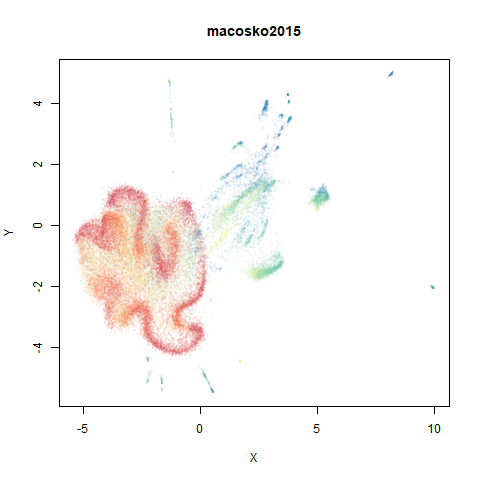
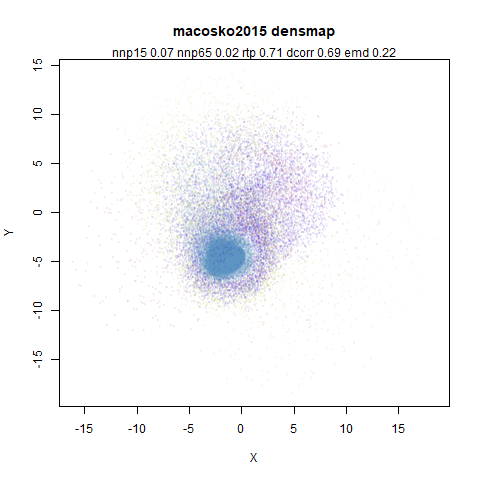
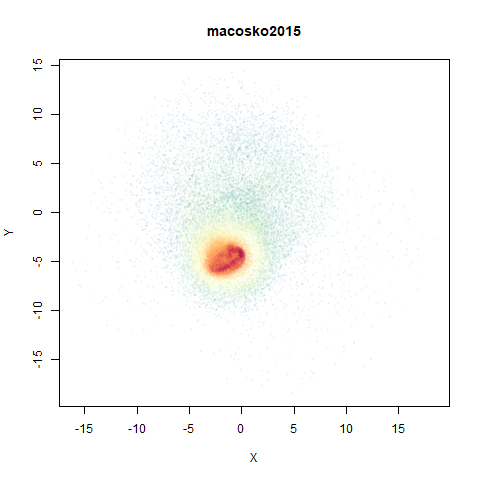
macosko2015

The macosko2015 RNAseq data.

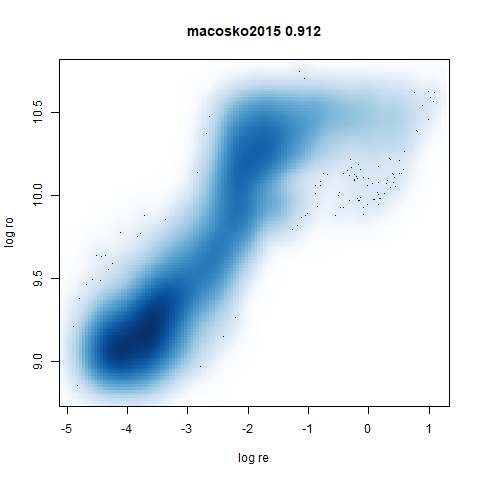This dataset (an RNA sequence dataset) isn’t a lot of fun to visualize with vanilla UMAP, but densMAP does not improve matters.

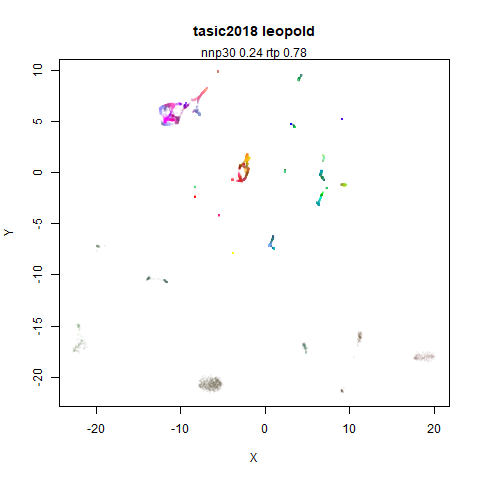
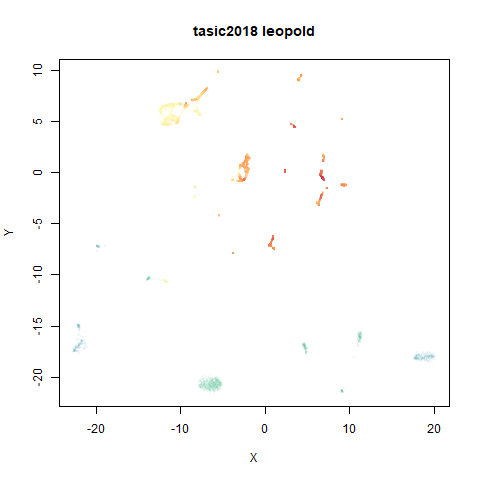
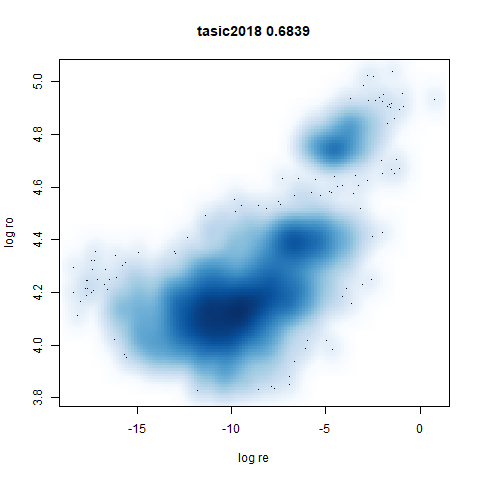
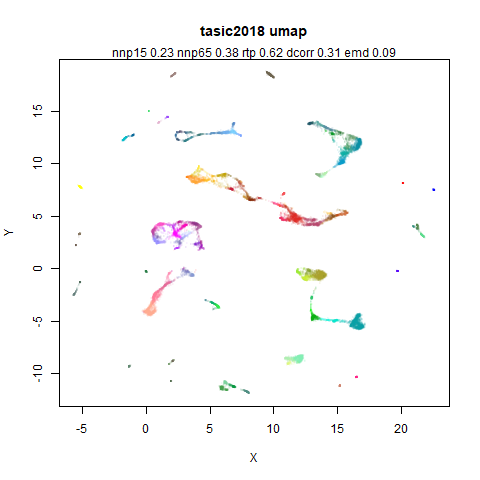
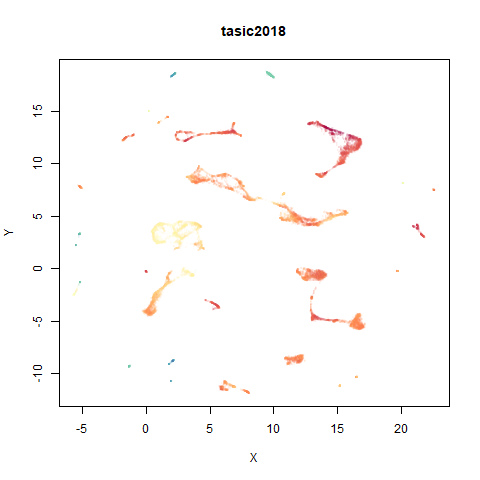
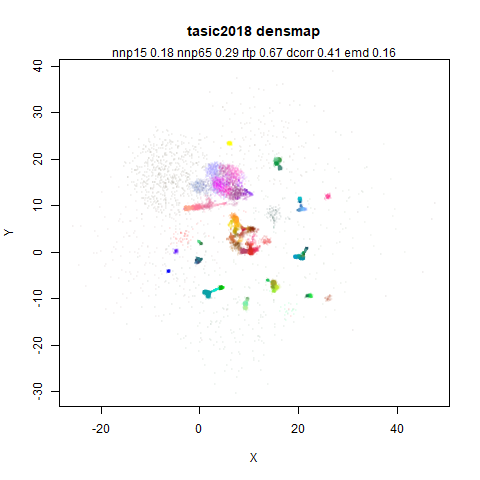
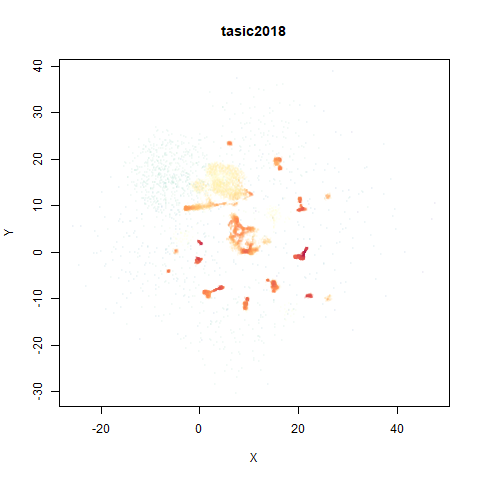
tasic2018

RNAseq data from the Allen Brain Atlas originally reported by Tasic and co-workers.

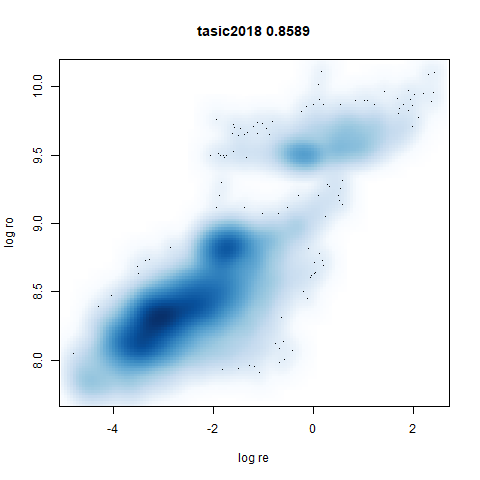Another RNAseq dataset, densMAP has a very interesting effect on the cluster sizes, but because some of the clusters have a very low density, this has the effect of squashing the other into the center of the plot.

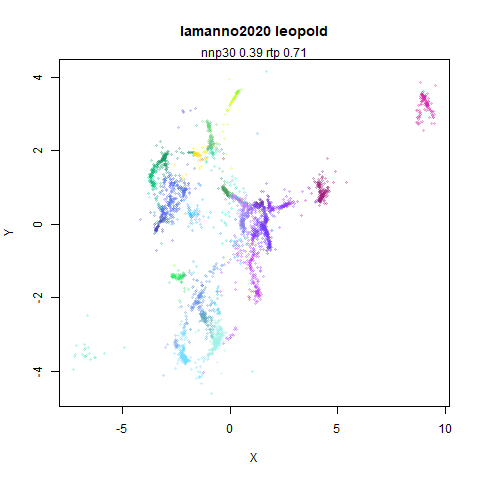
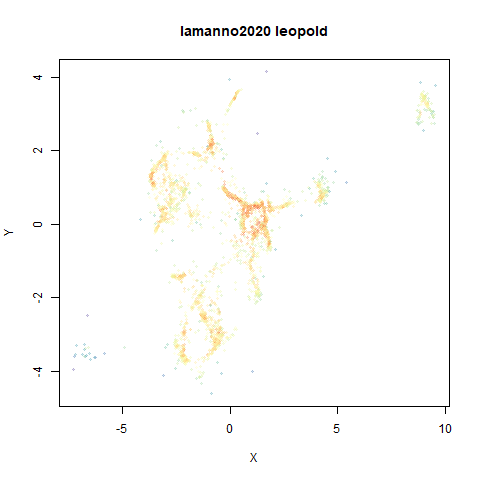
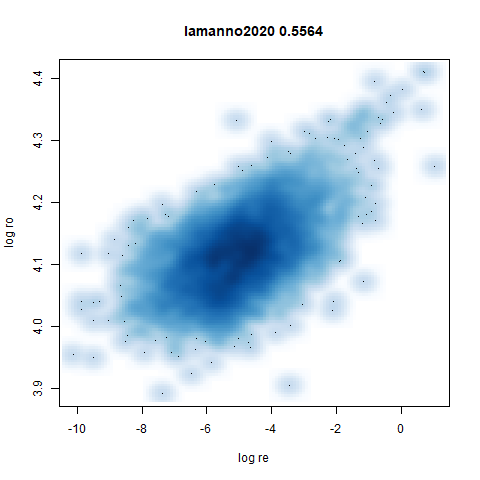
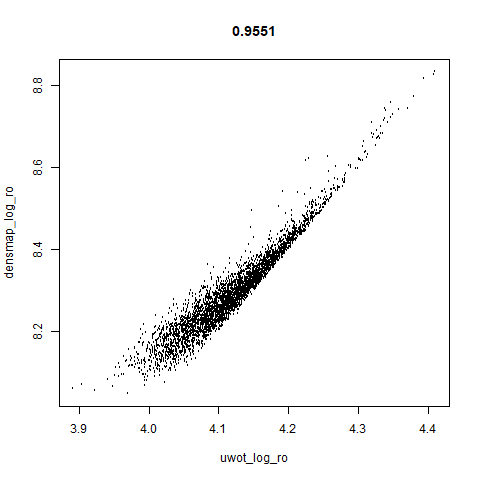
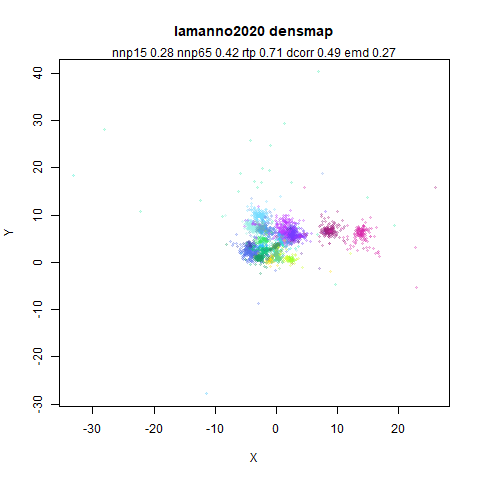
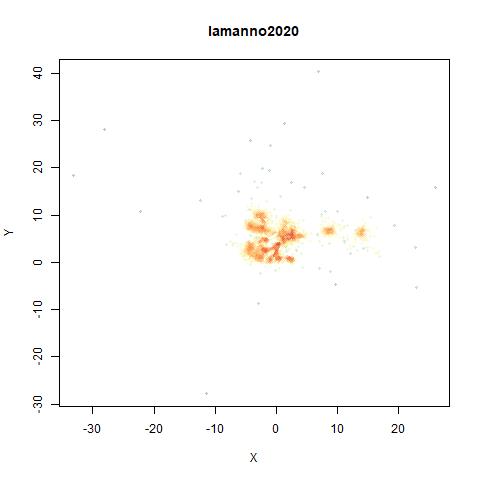
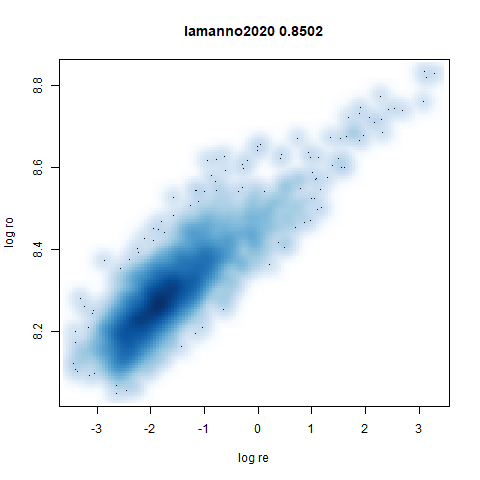
lamanno2020

Another RNASeq data, found via the Picasso example notebook. I think the publication reference is https://doi.org/10.1038/s41586-021-03775-x (was published at biorXiv in 2020).

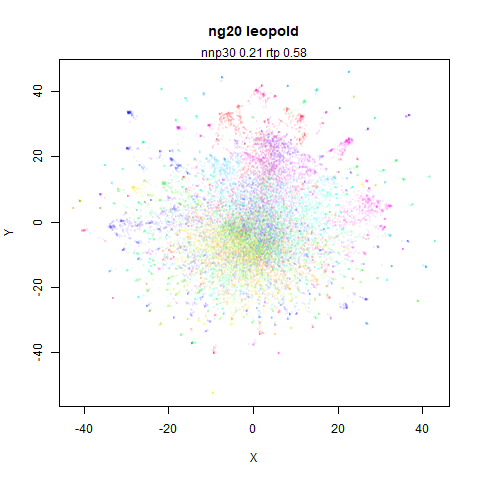
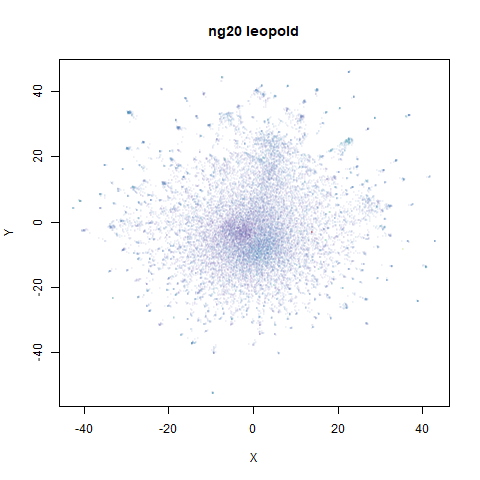
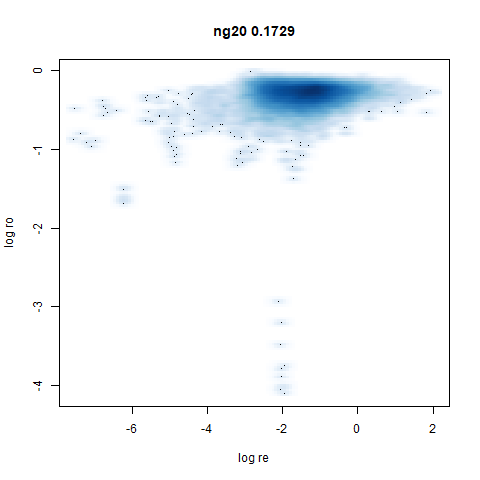
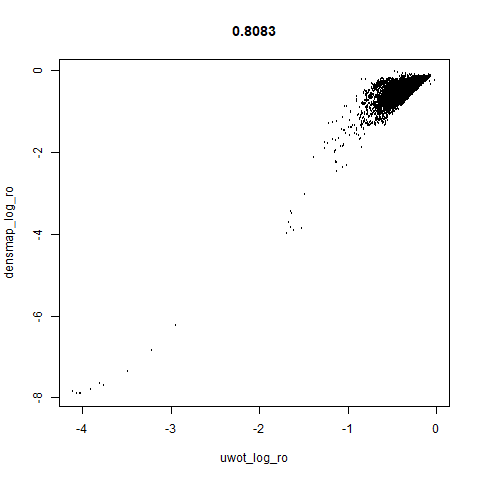
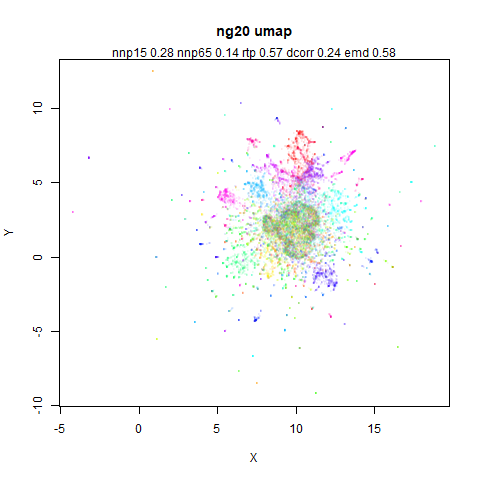
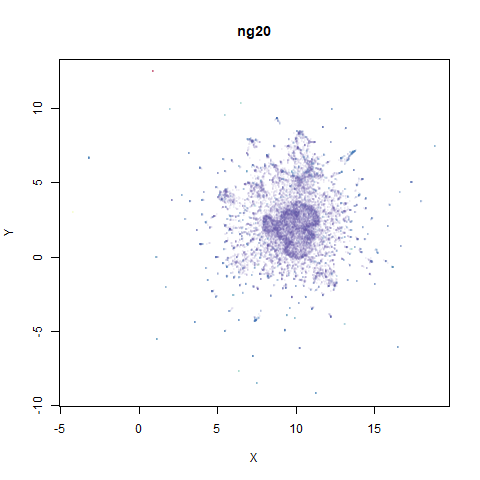
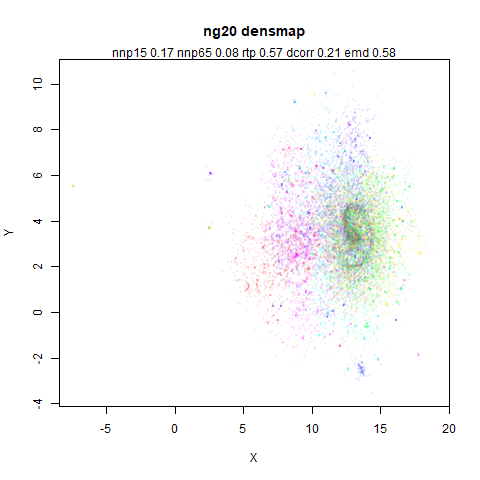
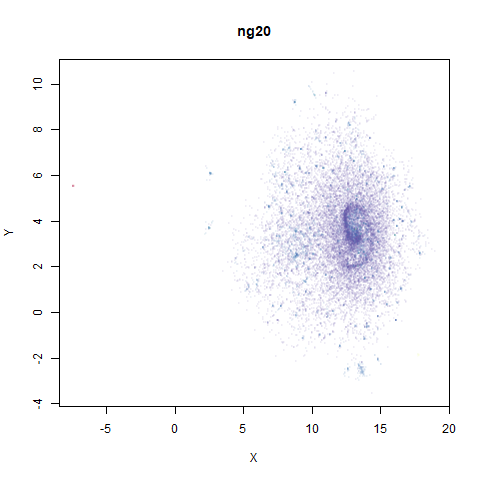
ng20

The 20 Newsgroups dataset, which I manually converted into a dense 3000D PCA result: see this gist.

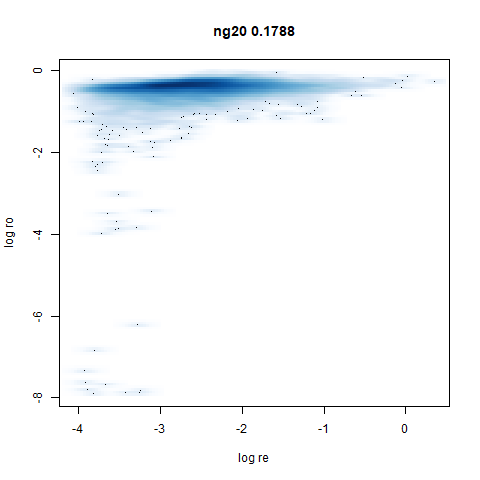densMAP noticeably has a hard time mapping the local radii to the 2D output.

What I take away from all this:

• densMAP does a good job at maintaining the correlation of input and output radii. The only time it fails is with the 20 Newsgroups dataset.
• A good correlation doesn’t necessarily mean a helpful static visualization. Some of the results have some clusters which are highly dispersed which may reflect the true relationship of densities but makes it hard to actually see the cluster, and the rest of the data gets crushed into the middle of the plot. That’s not necessarily a problem if you have an interactive plot and can pan and zoom. Or you can change the regularization value of dens_lambda. I didn’t try that but I have no reason to doubt a satisfying value can be found for any of the datasets where I didn’t like the output with default settings.

But I don’t currently want to implement densMAP because it involves adding lots of extra code, much of it in C++ and I am very lazy.

Approximating densMAP

Here’s my pitch for an approximation to densMAP, which I have named the Lightweight Estimate of Preservation of Local Density (Leopold).

For the input radii, as part of the smooth k-nearest neighbor distances routine we already calculate $\rho$ which is the distance to the nearest neighbor of each item in the dataset (subject to the local_connectivity constraint). Additionally, we also calculate $\sigma$ which is a normalization factor used with the neighbors at distance greater than $\rho$. It must have units of distance, and the larger the distances to the neighbors, the larger $\sigma$ gets. So I propose the following definition for the local radius:

$$R_i = \rho + \sigma$$

The biggest difference between this definition of the local input radii is that I haven’t bothered to square the distances (it doesn’t make much difference for leopold) and that the values for $\sigma$ and $\rho$ are calculated before the symmetrization of the UMAP input edge weights. So these values are missing the influence of observations outside the initial k-nearest neighborhood graph.

For the output radii, I know from looking at the output weight function parameters, that increasing the a parameter makes the clusters in a UMAP plot shrink, and vice versa. So let’s use that as measure of the output density, i.e. the inverse of the local radius. As every point has its own radius, the value for a given weight between points $i$ and $j$ will be the geometric mean of the two radii:

$$w_{ij} = 1 / \left(1 + \frac{d_{ij}^2}{\sqrt{r_i r_j}} \right)$$

where $r_i$ is a scaled version of the input radius $R_i$ suitable for the lower dimensional space. This is a similar sort of scaling to that used by Zelnik-Manor and Perona for “self-tuning” spectral clustering, and also recommended for local scaling to reduce hubness in high dimensional space by Schnitzer and co-workers.

The scaling from input to output space is not sophisticated: I have observed that for typical values of $b$ used in UMAP, a usable range of $a$ values are between 0.01 (very diffuse clusters) and 100 (very tight clusters), so we will just map the inverse of the input local radii to that range.

The final adjustment to this is that it would be good to introduce a parameter that controls how much of the range of a is used in the output and thus how big a disparity of the input radii is reflected in the output. To that end, there is an adjustable parameter for leopold: a dens_scale parameter. Set it to 1 and it uses all the available range of a. Set it to 0 and you get plain old UMAP back, with a fixed global value of a as specified by the user (or via the spread and min_dist parameters). Intermediate values get intermediate results.

In my mind this scaling of the radii is straightforward, but looking up at that description maybe it’s not. The procedure is:

1. Define the minimum log density as $a \times 10^{-2s}$ where $a$ is the UMAP a parameter for the output and $s$ is the den_scale parameter.
2. Define the maximum log density as $a \times 10^{2s}$.
3. Range scale $\log \left(1 / R_i \right)$ between the minimum and maximum log density. Call that range scaled log density $\Delta_i$
4. $a_i = \sqrt{ \exp \left( \Delta_i \right) }$.
5. The leopold output weight function is $w_{ij} = 1 / \left( 1 + a_i a_j d_{ij}^2 \right)$.

The Advantage of leopold

The main advantage is for me: to implement this I don’t have to write much new code: $\rho$ and $\sigma$ are already calculated and implementing the per-observation value for a in the output function requires creating a new version of the umap gradient routine that expects a vector of values rather than a scalar. This is a lot less work than implementing densMAP.

The Disadvantage of leopold

It’s all a bit approximate. But all I really want from this technique is that it makes the dense clusters get smaller and the diffuse clusters get bigger. The exact changes seem less important to me as long as they are vaguely sensible. I don’t claim to have a good sense of what I expect to see when a blob of data with an intrinsic dimensionality of $d$ and a radius of $r$ is embedded into 2D versus one with an intrinsic dimensionality of $d + 5$ but a radius of $r / 2$. Even if that was accurately embedded, would it even look sensible let alone helpful?

Results

Here are some plots using leopold. I used exact nearest neighbors for these results as nearest neighbor calculations are usually the slowest part of UMAP. The following deviations from default parameters were used: min_dist = 0.1 to be closer to the Python UMAP results. For consistency with densMAP, n_neighbors = 30 except for subset_clusters which uses n_neighbors = 150. Also to be consistent with densMAP, an extra 200 epochs on top of the usual default n_epochs was used.

In the plots below:

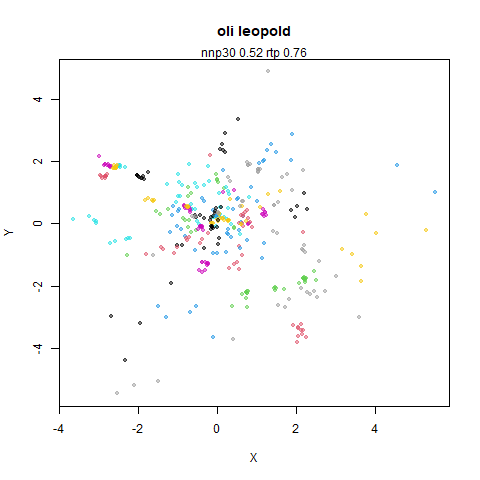
top left: the output of running leopold,

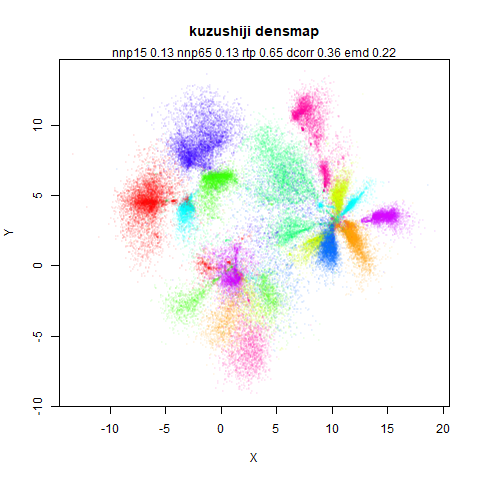
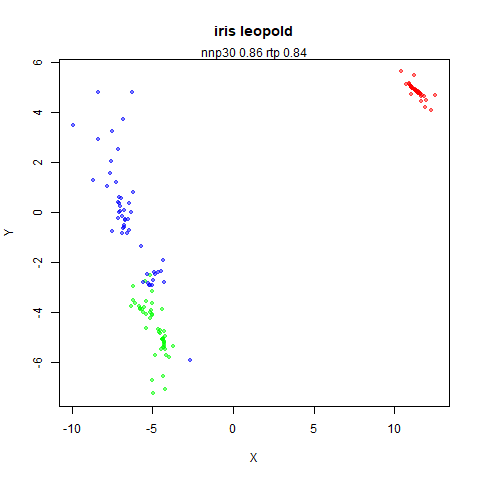
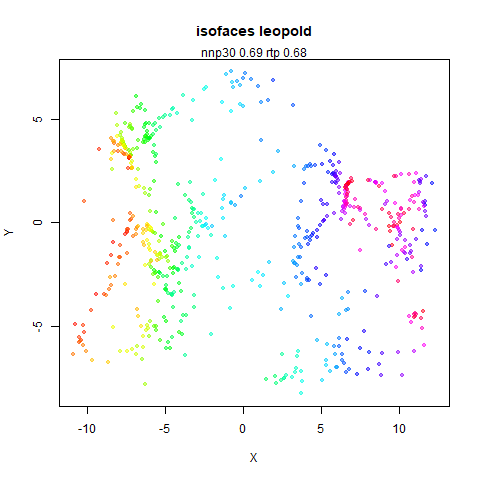
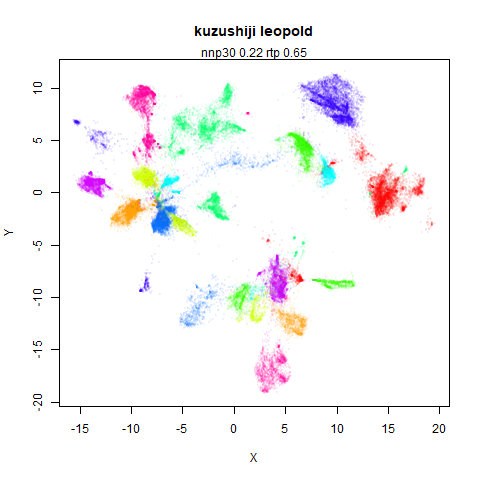
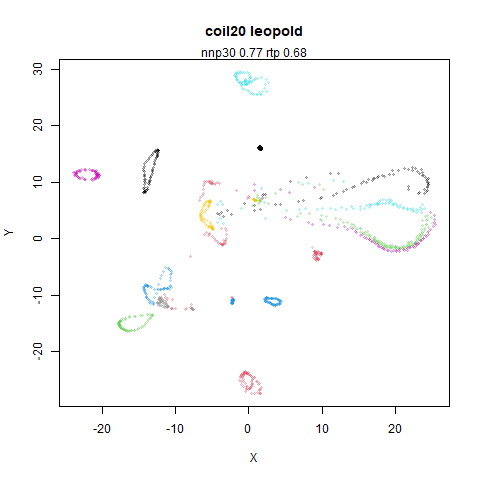
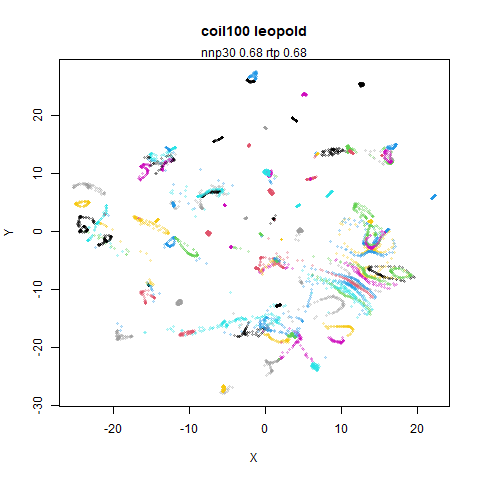
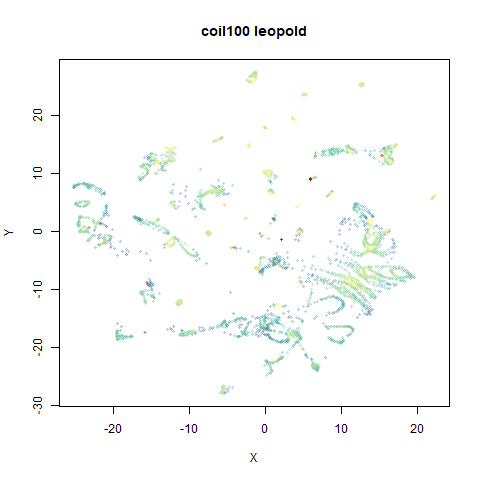
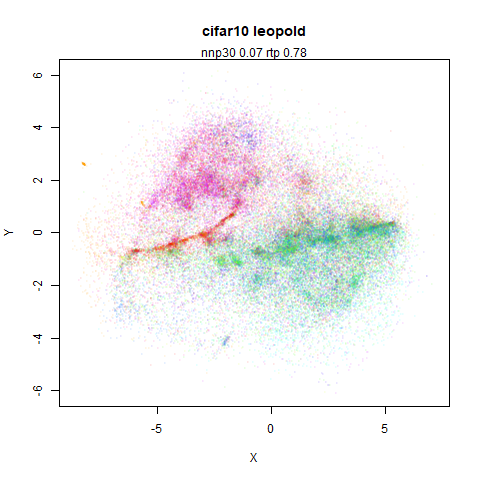
• Top left: the leopold results colored by the typical label for that dataset.
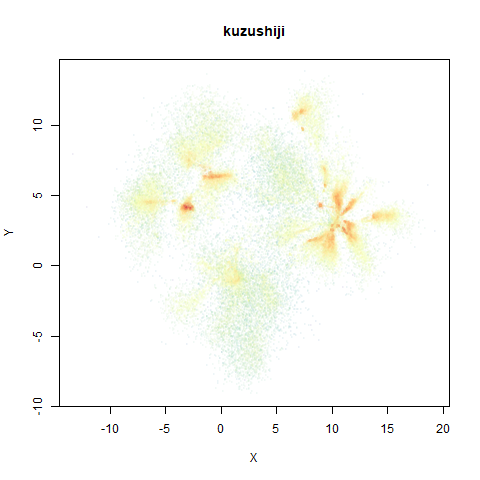
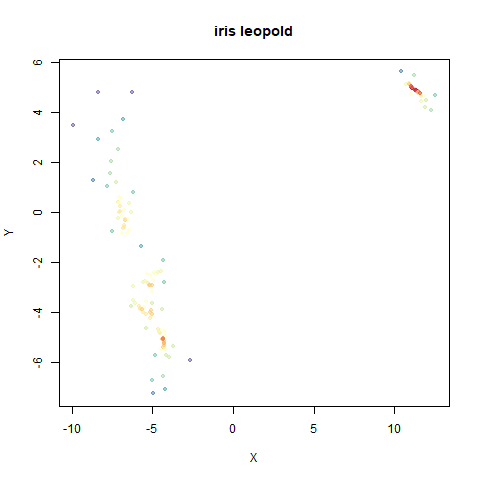
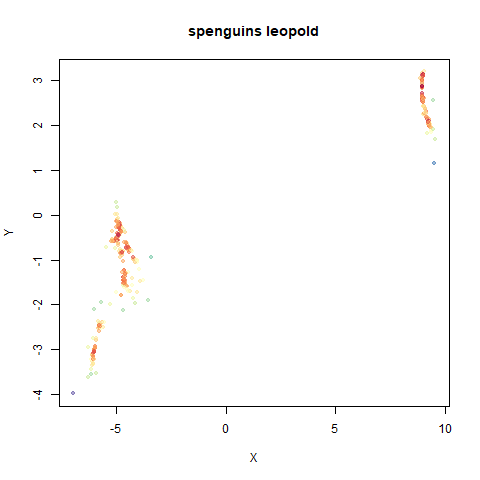
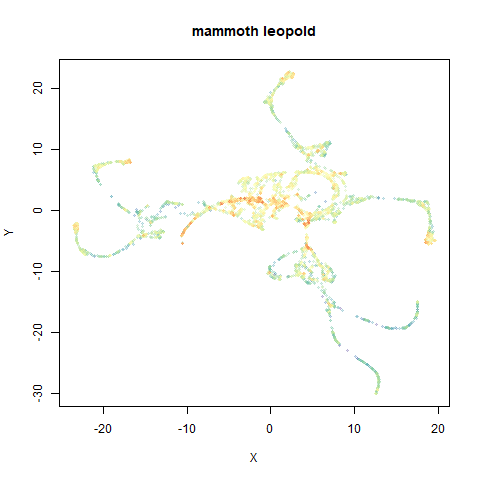
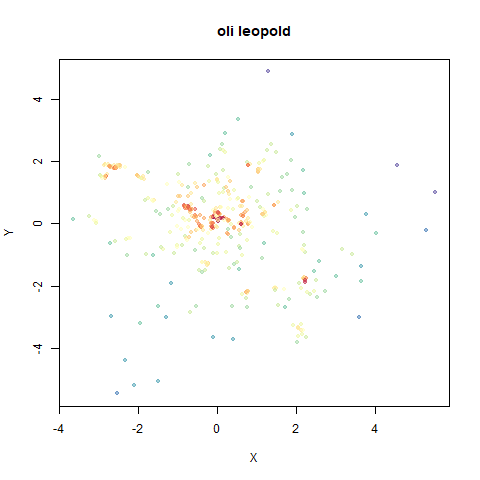
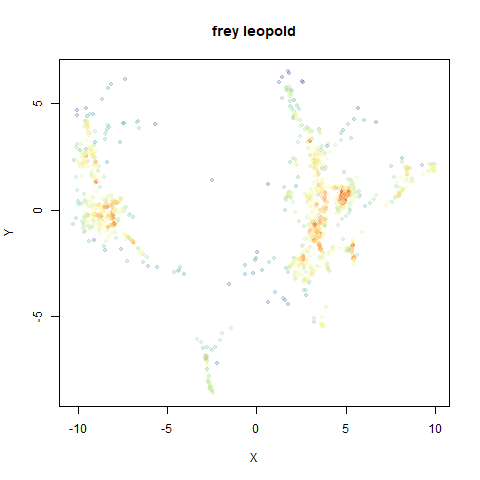
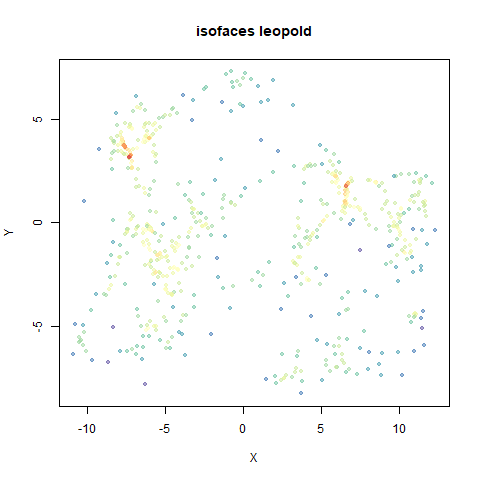
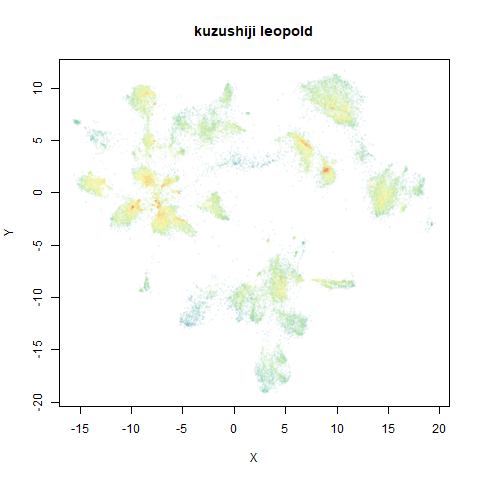
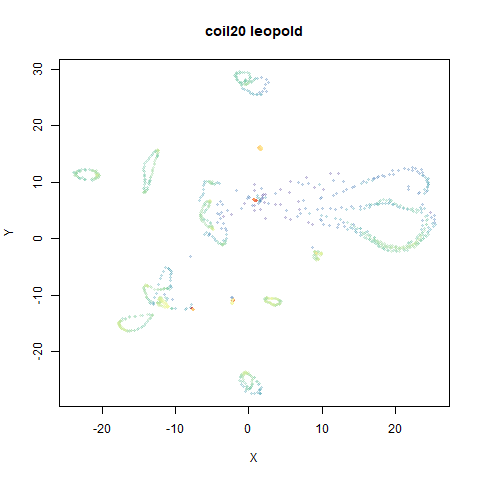
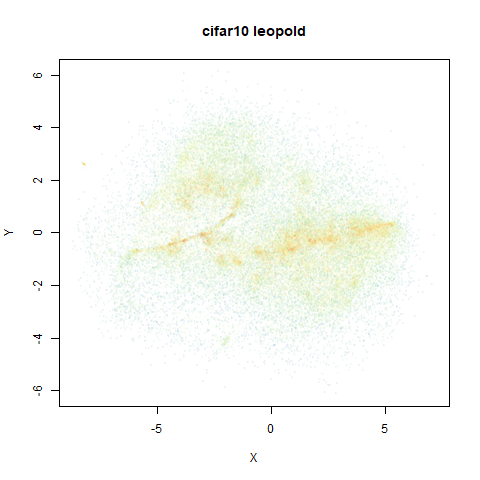
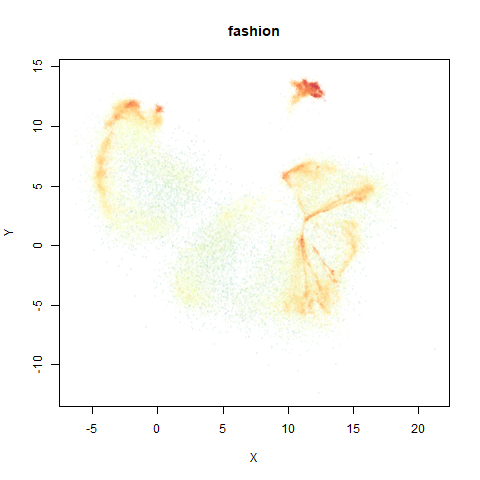
• Top right: UMAP results with each point colored by the log of the input local radius, using the ColorBrewer Spectral palette. Red means a small radius, blue means a large radius. This should show areas that densMAP is likely to contract or expand, respectively.
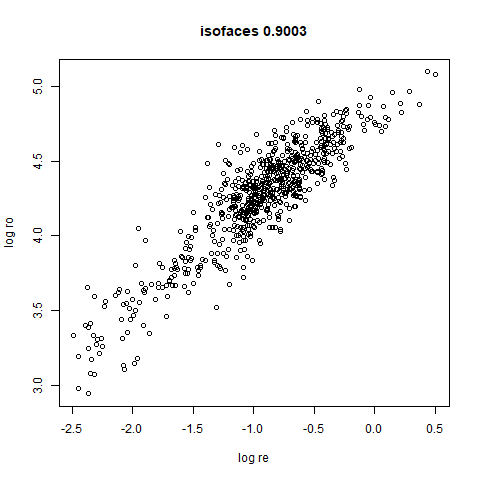
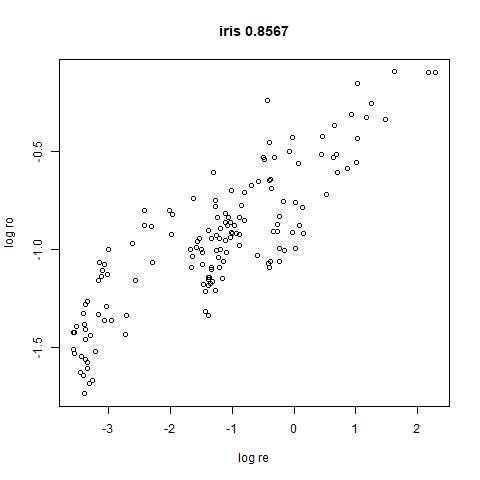
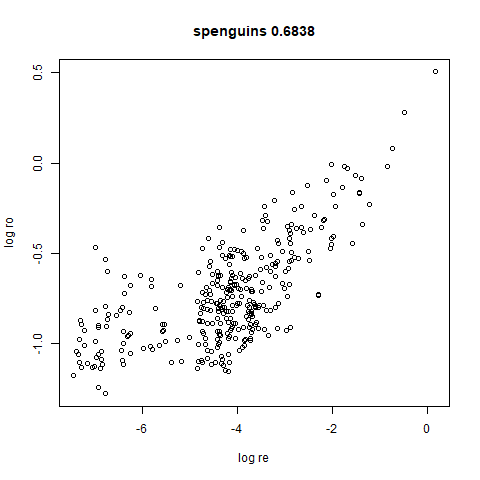
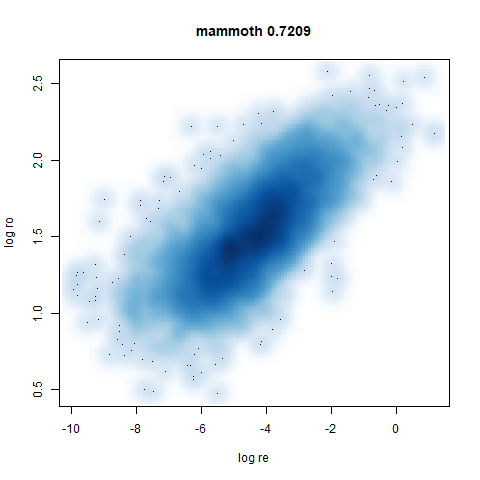
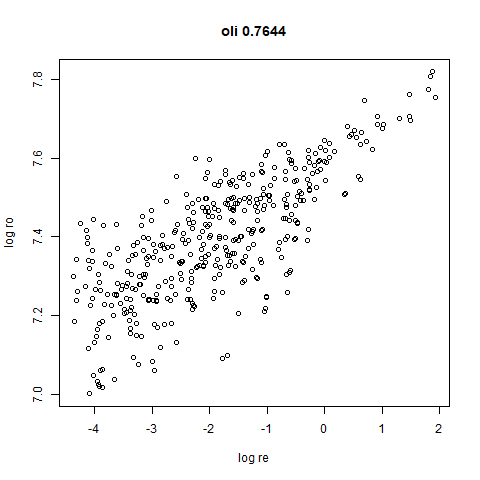
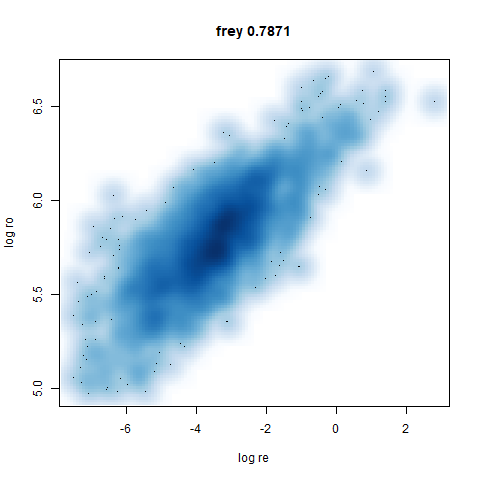
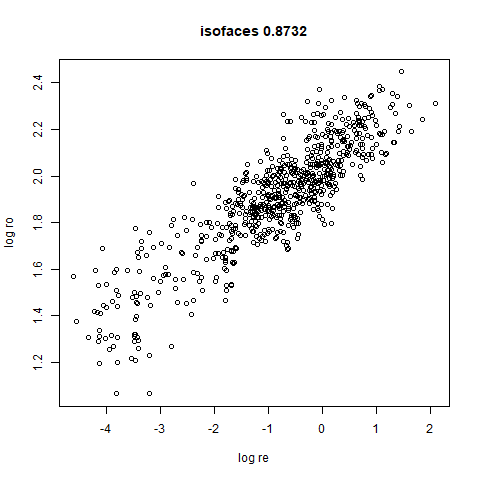
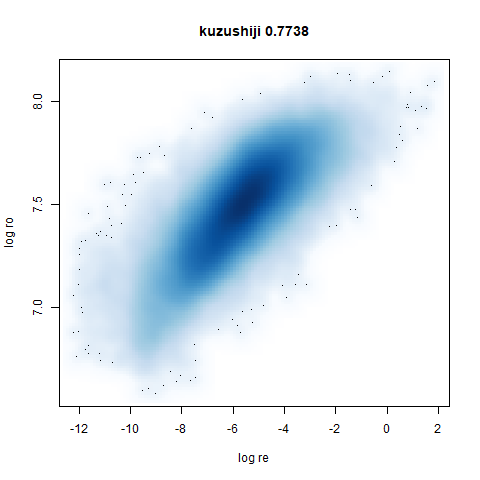
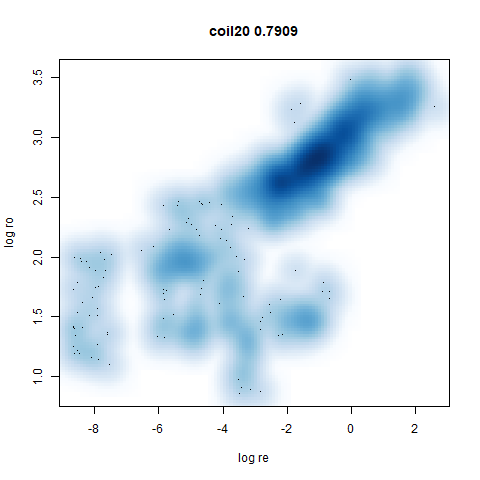
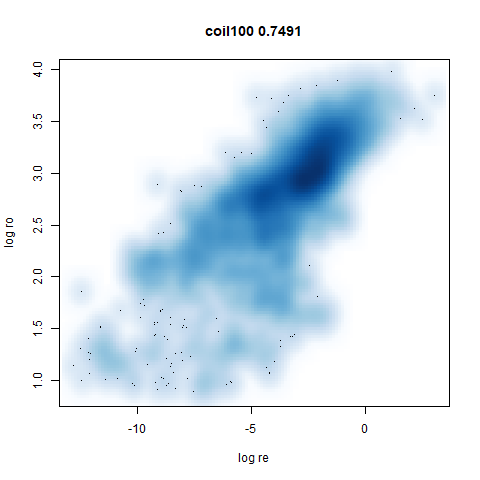
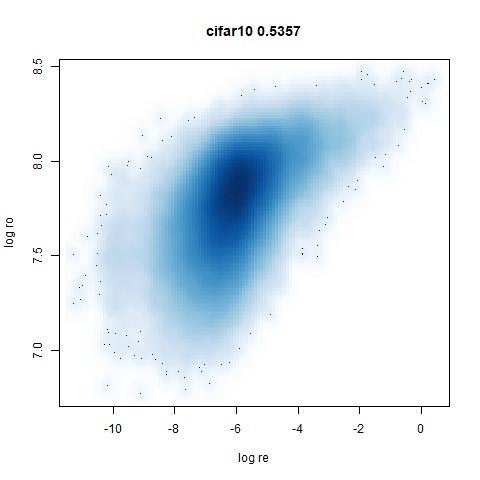
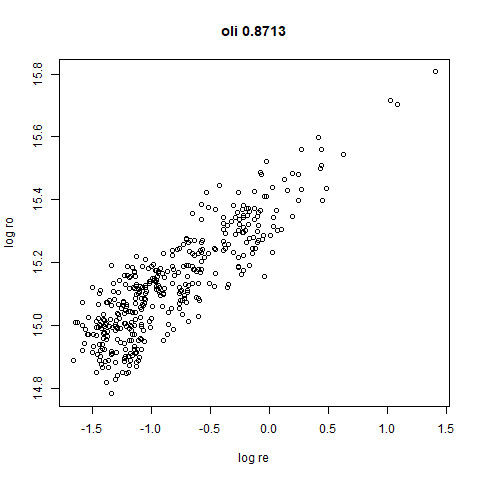
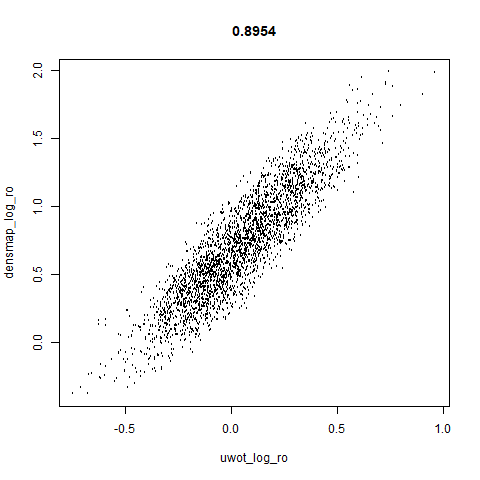
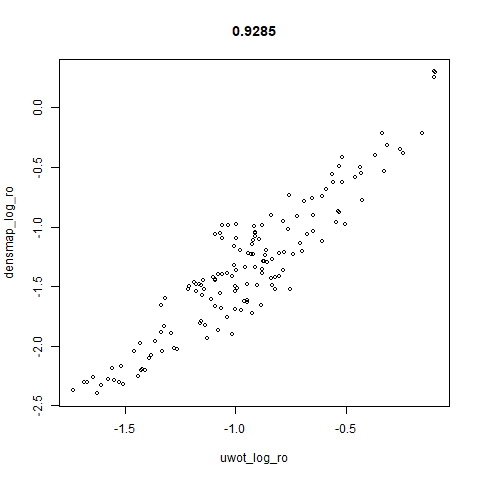
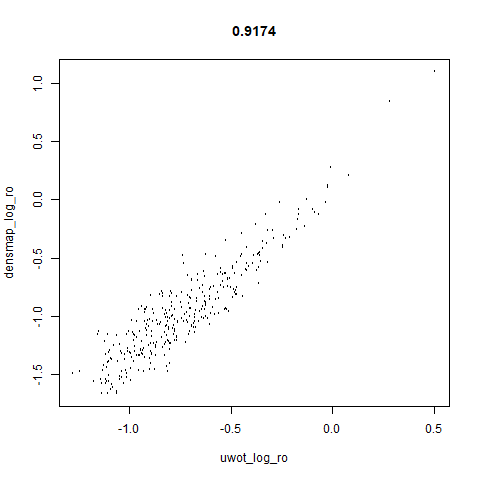
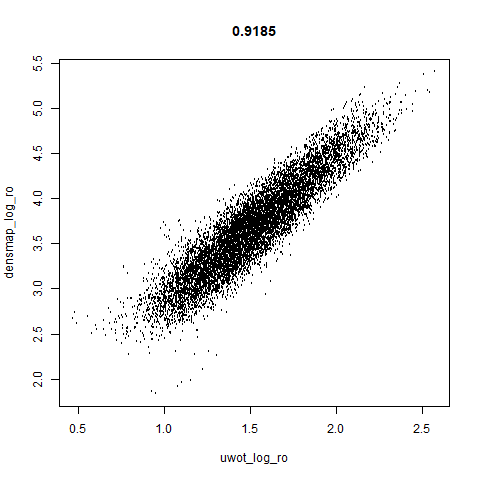
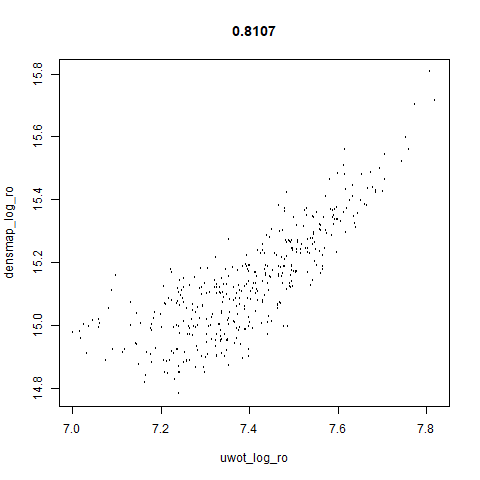
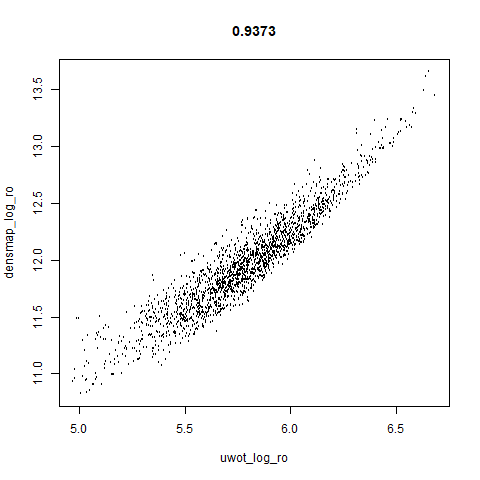
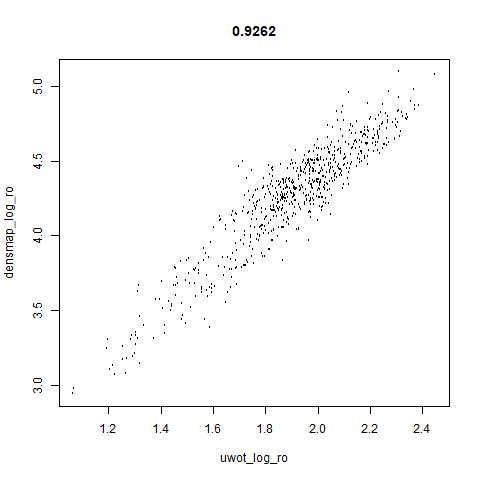
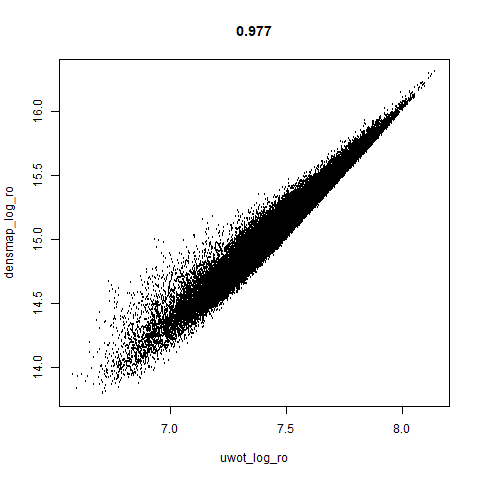
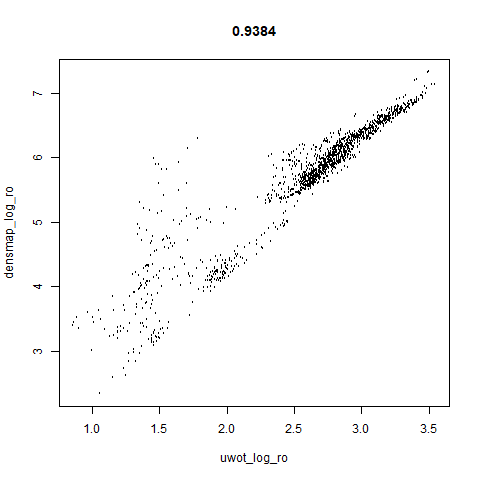
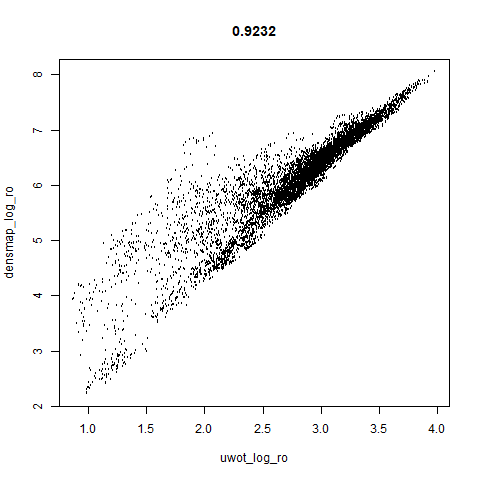
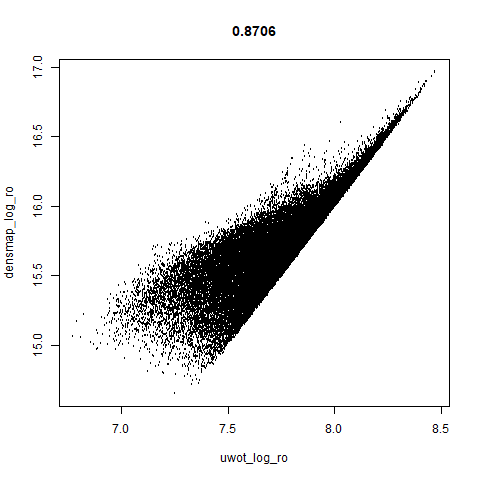
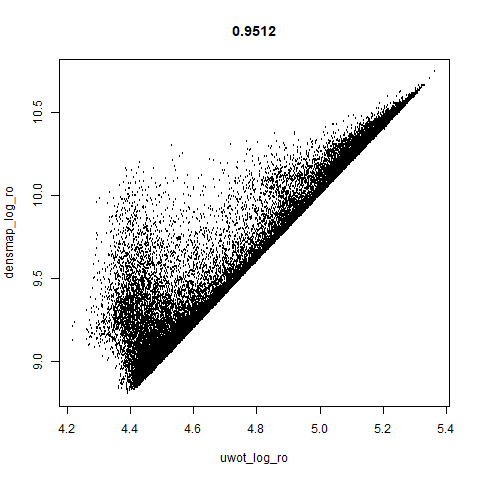
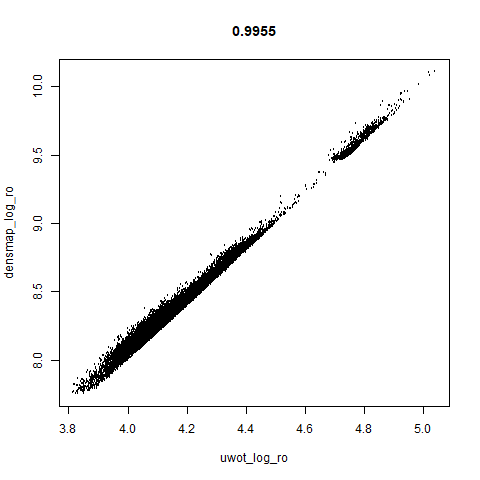
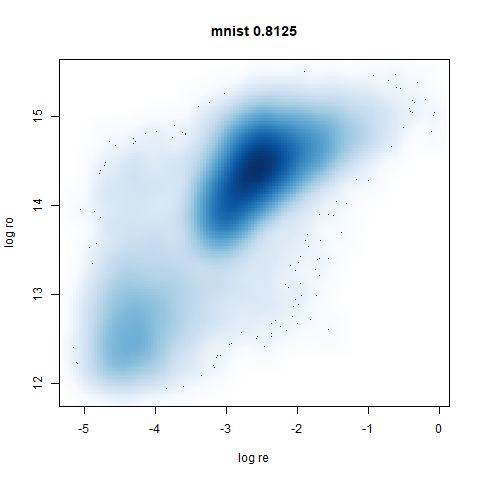
• Bottom left: a plot of the log of the input local radii vs the log output radii and the Pearson correlation between them. When there were more than 1000 points, I used smoothScatter to plot the results.
• Bottom right: a plot of the log of the densmap input local radii against the leopold equivalent ($\rho + \sigma$). The number in the title is Pearson correlation. There’s no particular reason for the two measures of local radius to be the same, but they should show a similar trend.

For a lot of these datasets, I won’t have anything to say unless there is an interesting contrast or similarity with densMAP.

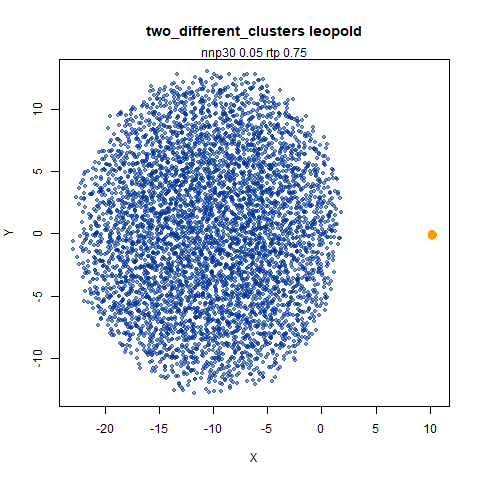
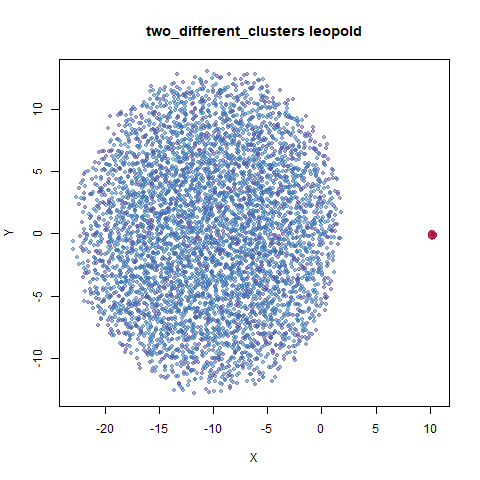
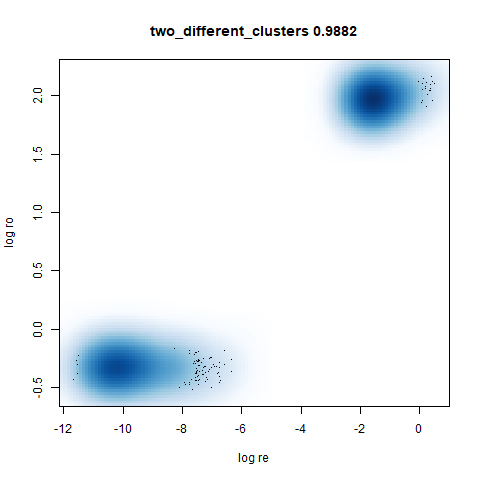
two_different_clusters

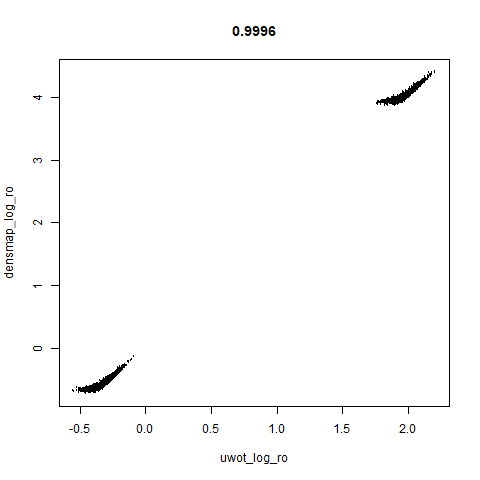leopold is able to produce two different sizes for the cluster, although the size disparity is much larger than for densMAP. This is due to the very bimodal nature of the standard deviations in this dataset. One cluster gets one end of the radii scale (highly disperse) and the second cluster gets the other (highly compact). Turning down dens_scale to something like 0.2 works well for this data set. But it doesn’t really matter as this is a very artificial dataset. As long as the clusters are the right relative size I am happy.

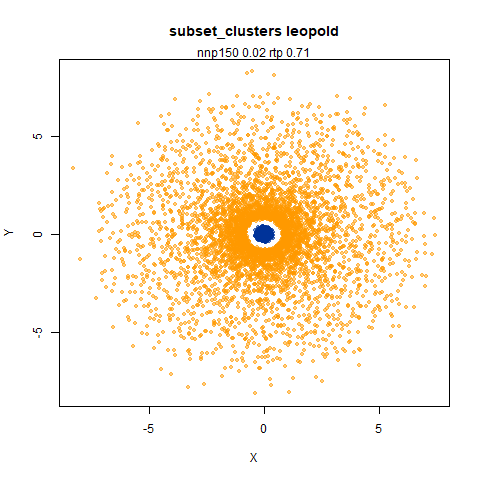
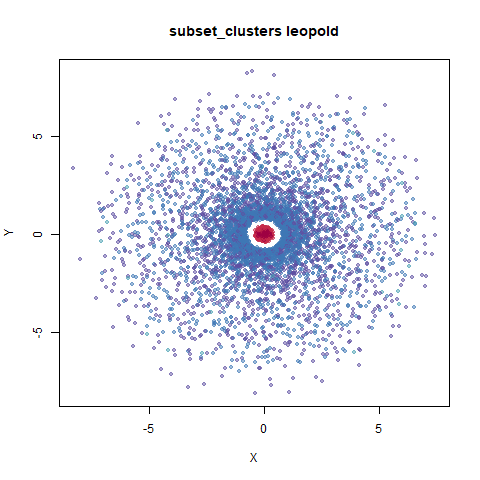
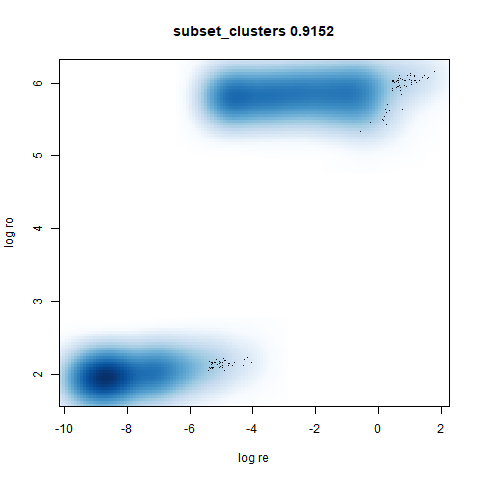
subset_clusters

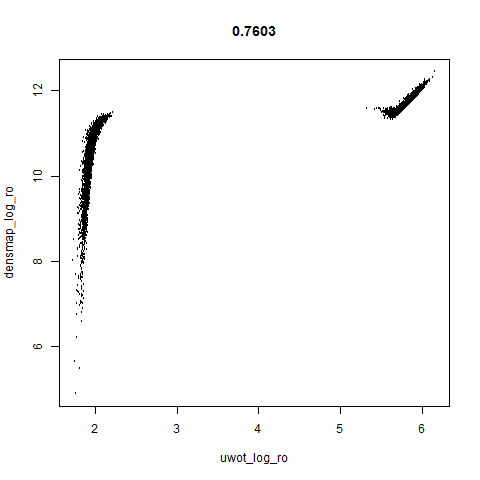This shows an interesting difference with densMAP: with densMAP, the outer yellow ring had a more uniform density, whereas for leopold there is a noticeable density gradient towards the center. I leave it up to you to decide if that is a good or a bad thing.

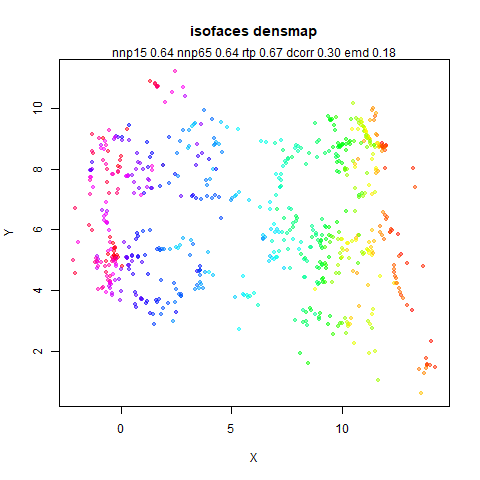
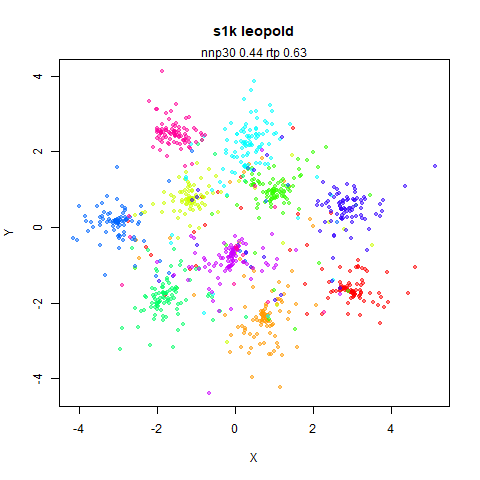
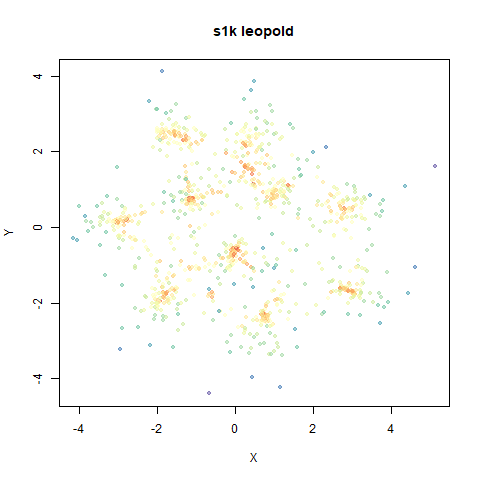
s1k

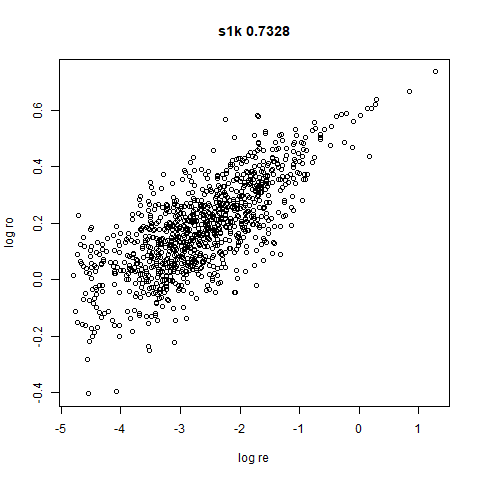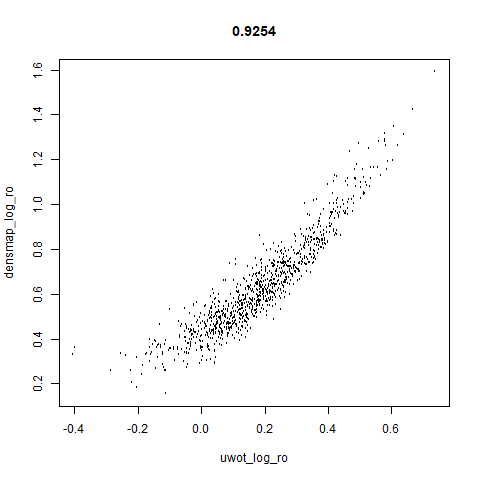The point that got pushed far away from the rest of the data in the densMAP plot is not as far away with leopold.

swissroll

Both this one and scurvehole seem pretty comparable with the densMAP results.

scurvehole

iris

spenguins

mammoth

If you compare this to densMAP, the extremities are much more diffuse than with leopold.

oli

frey

isofaces

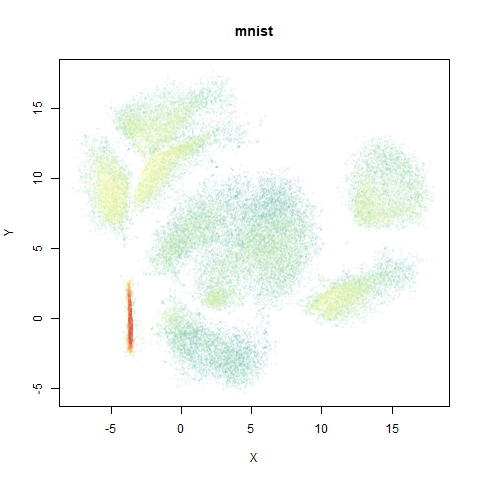
mnist

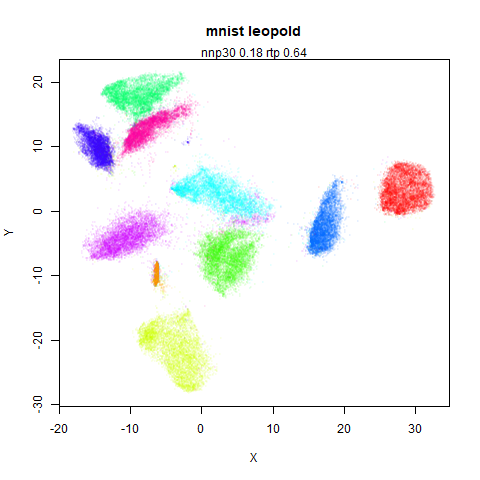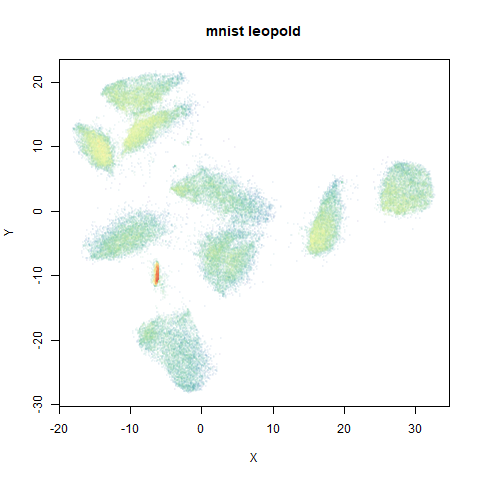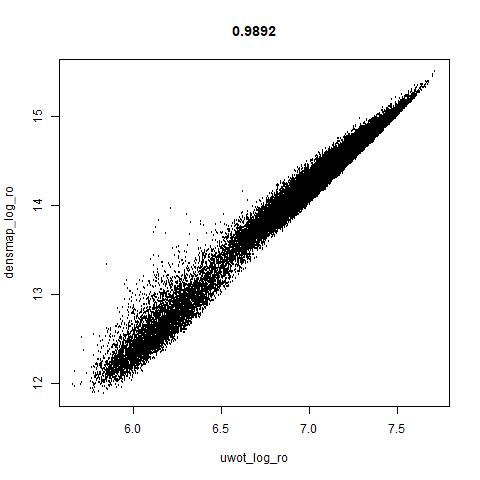The main thing I hoped to see was the orange ‘1’ cluster shrink. And it does. The yellow ‘2’ cluster has also noticeably grown. Changes are more subtle for the other clusters, but apart from the ‘1’ cluster their densities are all quite similar. I’m happy with this.

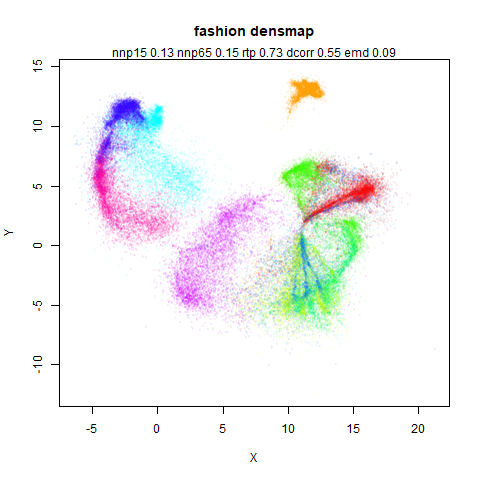
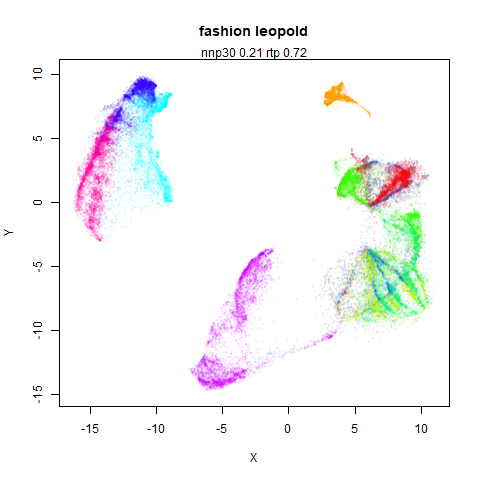
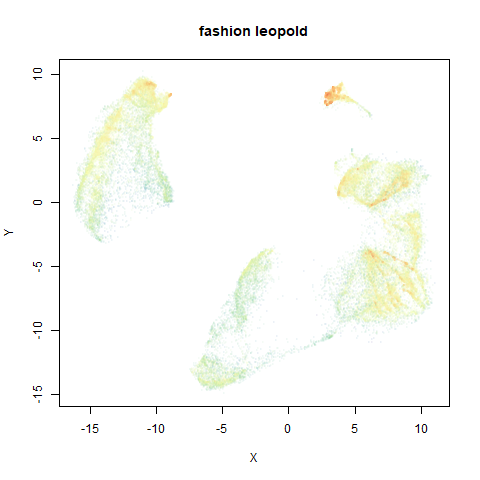
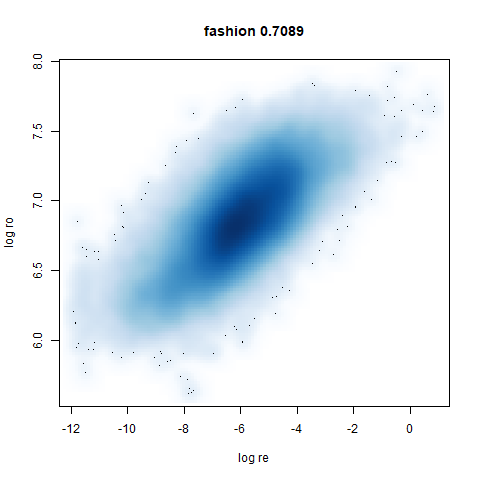
fashion

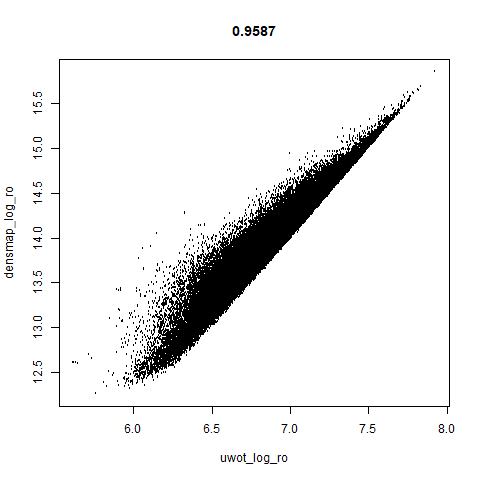leopold behaves in a densMAP-like way here too by shrinking the orange cluster. The clusters which densMAP expands are also larger here, but are not as diffuse as densMAP makes them. I personally prefer the leopold layout, but I am biased so you should probably just ignore me.

kuzushiji

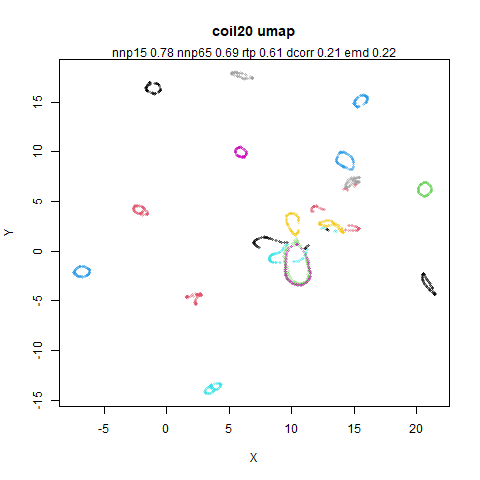
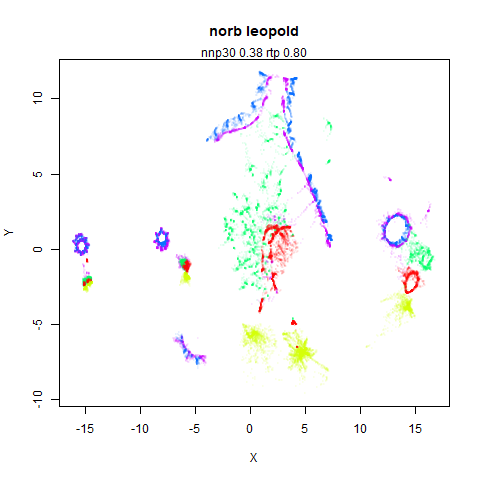
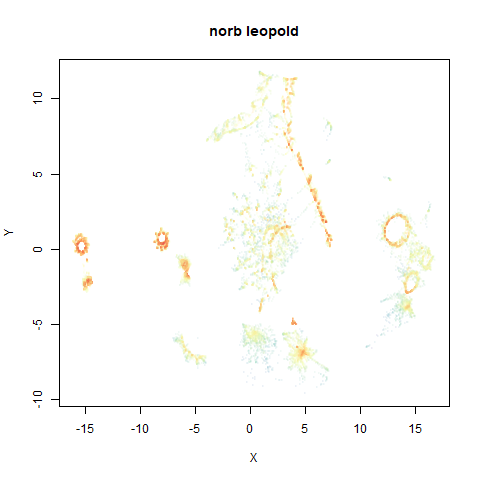
norb

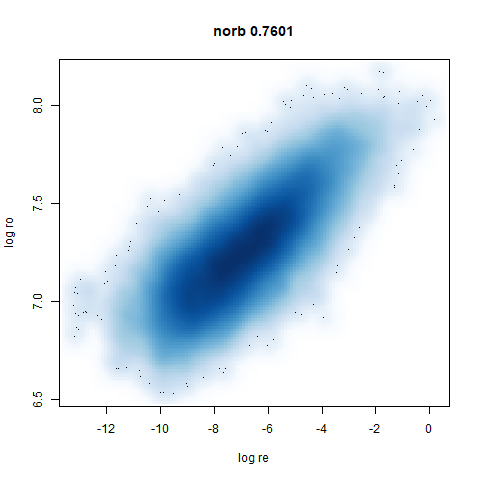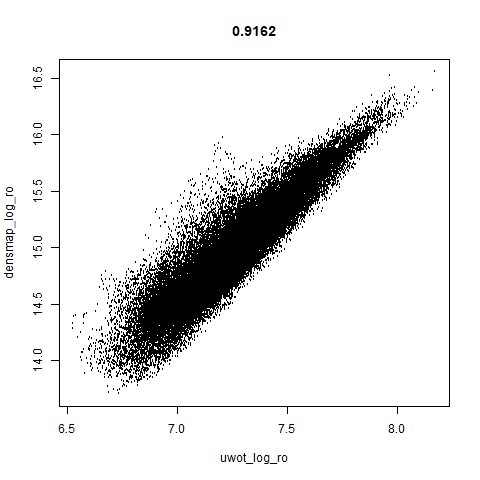This layout is fine, and maybe a bit neater than the UMAP one. But I still like the densMAP version better.

coil20

coil100

cifar10

macosko2015

I think the layout that leopold provides is more legible than the densMAP equivalent.

tasic2018

Another example where leopold produces a less compressed result, because the more diffuse clusters (e.g. the clusters at the bottom of the plot) are not as expanded.

lamanno2020

ng20

Does this layout look super-great? It does not. And nor can leopold reproduce the input radii in the output space, it seems in fact to be doing a worse job than densMAP. But it suffers less from outliers than densMAP which is something.

Conclusions

• I should probably be clear that I don’t think there’s anything wrong with densMAP.
• I am just currently too lazy to make all the changes in uwot it would need to be implemented. Hence leopold’s creation.
• Neither leopold’s definition of local radii or the results exactly map that of densMAP. So don’t go looking to reproduce densMAP plots exactly with it.
• I think the leopold results look fine. The dense clusters get smaller and the diffuse clusters get larger, although in the latter case not to the same extent as densMAP. However, that isn’t a big disadvantage from my perspective.
• densMAP does a better job in terms of the correlation between its input and output radii.
• Qualitatively, the densMAP and leopold results are quite similar.
• The correlations between the leopold definition of local radii and the densMAP version are pretty high for real datasets. So I venture to suggest they encode quite similar information.

If you want to use leopold in uwot:

• Set the dens_scale parameter to a value between 0 (exactly like UMAP) to 1 (use the full range of useful a values).
• Using leopold doesn’t seem to require extra epochs and you don’t need to worry about having to run normal UMAP for a number of epochs before applying leopold.
• Nor does it seem to benefit from a larger value of n_neighbors.
• I have re-run the results with n_neighbors = 15 and default n_epochs and not noticed a very big effect compared to the results here, so I am not showing them as there are already way too many images on this page.
• You can transform new data with models generated where dens_scale is set. When UMAP transforms new data, an adjusted local connectivity is used which affects both $\sigma$ and $\rho$ so the estimated values of $R_i$ are not as precise as I would like, but the effect seems to be quite small.
• Even if you don’t use the local radii to generate the UMAP layout, coloring the results by the log of localr is quite informative as to which parts of the embedding you would expect to shrink or expand.
• A conservative use of leopold would be to run UMAP normally, visualize the results coloring by localr and then if there are obvious clusters that are a lighter or darker hue, run with dens_scale = 1 from the current coordinates for a couple of hundred more epochs.

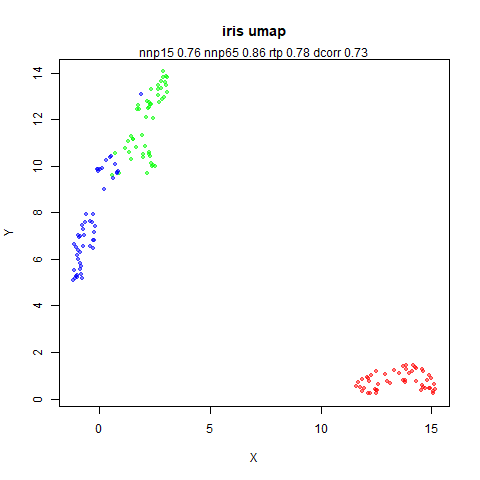
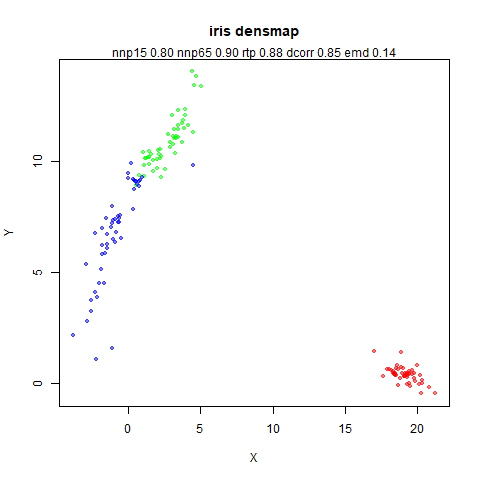
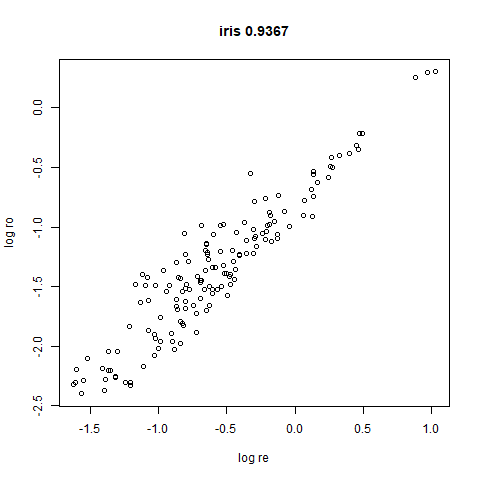
Here’s how you use it with iris:

iris_leopold <- umap(iris, dens_scale = 1)
# and if you want the local radii values
iris_leopold <- umap(iris, dens_scale = 1, ret_extra = c("localr"))