Skip to contents

Embedding New Data

Out of Sample Data

Source: vignettes/articles/embedding-new-data.Rmd
embedding-new-data.Rmd

Note: some of this information is repeated from the metric learning article, an article so poorly-titled that I was unable to find where I had discussed transforming new data. As requested by RoyiAvital, this article focuses only on tranforming new data into an existing embedding, and a description of how this is achieved.

To embed new data into an embedding so you should:

  • set ret_model = TRUE when running umap on the original data.
  • Provide the return value of that call to umap to the umap_transform function along with your new data.

How It Works

  1. Let’s say PP are the set of embedded points and there are NPN_P of them. Likewise there are new points to embed called QQ (could be as few as 1 point in Q).
  2. For a given new item to embed, qq, find the n_neighbors nearest neighbors from the already embedded dataset (i.e. find p1p_1`, p2p_2, …, pkp_k).
  3. Form the affinity matrix between the NQN_Q points to embed and the original NPN_P points. The affinity matrix is no longer square or symmetric but that doesn’t matter.
  4. Embed that as usual, where we want the Euclidean distance in the low-dimensional space to reproduce the affinities in the affinity matrix, via the usual UMAP cost function. Each pair of items is of the form (p,q)(p, q), i.e. it’s always one point from the original data and one from the new data. You don’t have pairs like (p,p)(p, p) or (q,q)(q, q).
  5. The only deviation from the standard way of doing things is that you don’t let the coordinates of any of the pp points update only the qq.

There are some minor differences to the parameters involved in the transform:

  1. Coordinates are initialized by taking the weighted average of the neighbors coordinates, where the weights are the affinities.
  2. In terms of calculating those affinities, the local connectivity is adjusted down by one. This is a rather obscure parameter that I rarely see (never?) being adjusted by users in either uwot or in other implementations. It controls the number of neighbors that are considered fully connected to a point (i.e. gets an affinity of 1.0). It’s usually set to one, so that means when transforming data, the local connectivity is set to 0. I suspect the reason for this is that because of the initialization: because the points are located close to its neighbors we don’t need to worry about having items which are very distant during the optimization so we don’t need to enforce closeness to a given point.
  3. The learning rate is set to a quarter of whatever it was during training.

Example

Let’s use the fashion MNIST dataset.

devtools::install_github("jlmelville/snedata")
fashion <- snedata::download_fashion_mnist()

The Fashion MNIST dataset contains 70,000 images of fashion items, in one of ten classes. A factor column, Label contains the id of each item (from 0 to 9) for backwards compatibility with the MNIST dataset, which Fashion MNIST is designed to be a drop-in replacement for. A more descriptive, but entirely equivalent, factor column, Description provides a short text string to describe the classes, e.g. the Description "Coat" and the Label 4 are equivalent.

fashion_train <- head(fashion, 60000)
fashion_test <- tail(fashion, 10000)

Training proceeds by running UMAP normally, but we need to return more than just the embedded coordinates. To return enough information to embed new data, we need to set the ret_model flag when we run umap. This will return a list. The embedded coordinates can be found as the embedding item.

Training Data

I am using the umap2 function here, but you can use umap or tumap as you wish. I am also making use of the rnndescent library for nearest neighbor search. This is also optional (just don’t set nn_method).

set.seed(1337)
library(rnndescent)
fashion_umap_train <- umap2(fashion_train, ret_model = TRUE, nn_method = "nndescent")

Test Data

To embed new data, use the umap_transform function. Pass the new data and the trained UMAP model. There’s no difference between using a standard UMAP model:

fashion_umap_test <- umap_transform(fashion_test, fashion_umap_train)

Here are the results:

Training data (60,000 points) Test data (10,000 points)
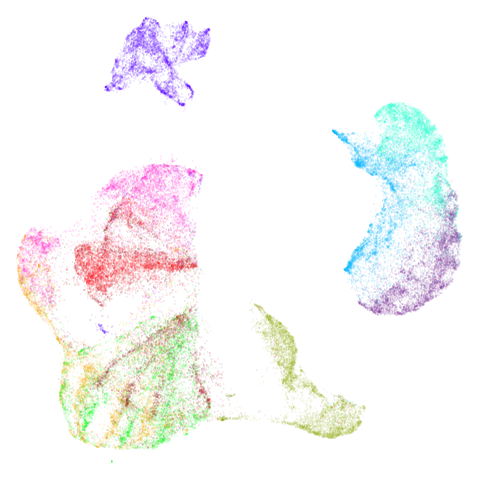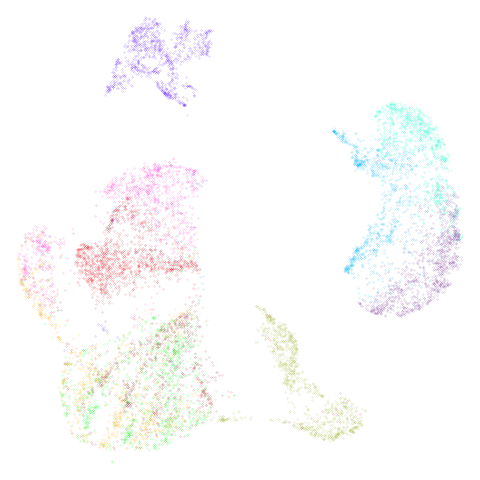Fashion UMAP Train Fashion UMAP Test

Looks pretty decent, although you could argue it’s not truly an “out of sample” example because the test data is all from the same distribution as the training data. If you made the test data an entire set of one labels, it is obviously not going to embed in the same place as it appear in the full embedding. You are also going to miss the interactions between the points within the test data.

Also, be aware that with small datasets you can get some odd looking ring effects from embedding the test data. See this issue for more details: https://github.com/jlmelville/uwot/issues/128 – in that issue I speculate that it’s due to false negatives being included in the negative sampling, i.e. actual close neighbors that should only be used for attractive forces.