Querying Data • rnndescent

library(rnndescent)

The usual pattern of usage for approximate nearest neighbors methods is:

Build some kind of index with input data.
Query that index with new data to find the nearest neighbors of your query.

This is how e.g. Annoy and hnswlib work. If you want just the k-nearest neighbors of the data you used to build the index in step 1, then you can just pass that data as the query in step 2, but rnndescent provides some specialized functions for this case that are slightly more efficient, see for example nnd_knn and rpf_knn. Nonetheless, querying the index with the original data can produce a more accurate result. See the hubness vignette for an example of that.

Below we will see some of the options that rnndescent has for querying an index.

For convenience, I will use all the even rows of the iris data to build an index, and search using the odd rows:

iris_even <- iris[seq_len(nrow(iris)) %% 2 == 0, ]
iris_odd <- iris[seq_len(nrow(iris)) %% 2 == 1, ]

Brute Force

If your dataset is small enough, you can just use brute force to find the neighbors. No index to build, no worry about how approximate the results are:

brute_nbrs <- brute_force_knn_query(
  query = iris_odd,
  reference = iris_even,
  k = 15
)

The format of brute_nbrs is the usual k-nearest neighbors graph format, a list of two matrices, both of dimension (nrow(iris_odd), k). The first matrix, idx contains the indices of the nearest neighbors, and the second matrix, dist contains the distances to those neighbors (here I’ll just show the first five results per row):

lapply(brute_nbrs, function(m) {
  head(m[, 1:5])
})
#> $idx
#>      [,1] [,2] [,3] [,4] [,5]
#> [1,]    9   20   14    4   25
#> [2,]   24    2   23   15    1
#> [3,]   19    9    4   20   14
#> [4,]   24    6   15    2   19
#> [5,]    2    7   24   23   15
#> [6,]   14   10    3   16   11
#> 
#> $dist
#>           [,1]      [,2]      [,3]      [,4]      [,5]
#> [1,] 0.1000000 0.1414213 0.1414213 0.1732050 0.2236068
#> [2,] 0.1414213 0.2449490 0.2645753 0.3000001 0.3000002
#> [3,] 0.1414213 0.1732050 0.2236066 0.2449488 0.2449488
#> [4,] 0.2236068 0.3000002 0.3162278 0.3316627 0.4123106
#> [5,] 0.2999998 0.3464101 0.3605550 0.4242641 0.4690414
#> [6,] 0.2828429 0.3316626 0.3464102 0.3605551 0.3605553

Random Projection Forests

If you build a random projection forest with rpf_build, you can query it with rpf_knn_query:

rpf_index <- rpf_build(iris_even)
rpf_nbrs <- rpf_knn_query(
  query = iris_odd,
  reference = iris_even,
  forest = rpf_index,
  k = 15
)

See the Random Partition Forests vignette for more.

Graph Search

See (Dobson et al. 2023) for an overview of graph search algorithms, which can be described as a greedy beam search over a graph: to find the nearest neighbors, you start at a candidate in the graph, find the distance from that candidate to the query point, and update the neighbor list of your query accordingly. If the candidate made it into the neighbor list of the query, this seems like a promising direction to go in, so add the candidate’s neighbors to the list of candidates to explore. Repeat this until such a time as you run out of candidates. You may want to explore the neighbors of the candidate even if it doesn’t make it onto the current neighbor list, if its distance is sufficiently small. How much tolerance you have for this controls how much back-tracking you do and hence how much exploration and the amount of time you spend in the search.

graph_knn_query implements this search. At the very least you must provide a reference_graph to search, the reference data that built the reference_graph (so we can calculate distances), k the number of neighbors you want, and of course the query data:

graph_nbrs <- graph_knn_query(
  query = iris_odd,
  reference = iris_even,
  reference_graph = rpf_nbrs,
  k = 15
)

If you aren’t using the metric = "euclidean", you should also provide the same metric that you used to build the reference_graph. The default metric is always "euclidean" for any function in rnndescent so it’s not provided in the examples here.

There are some other parameters you will want to tweak in any real world case that merit some deeper discussion.

`n_threads`

n_threads controls how many threads to use in the search. Be aware that graph_knn_query is designed for batch parallelism, and each thread will be responsible for searching a subset of the query points. This means that in a streaming context, where queries to search are likely to arrive one at a time, you won’t get any speed up from using multiple threads.

`epsilon`

epsilon controls how much exploration of the neighbors of a candidate to do, as suggested by (Iwasaki and Miyazaki 2018). The default value is 0.1, which is also the default of the NGT library. The larger the value, the more back-tracking is permitted. The exact meaning of the value is related to how large a distance is considered “close enough” the current neighbor list of the query to be worth exploring.

epsilon = 0.1 means that the query-candidate distance is allowed to be 10% larger than the largest distance in the neighbor list. If you set epsilon = 0.2, for example, then the query-candidate distance is allowed to be 20% higher than the largest distance in the neighbor list and so on. If you set epsilon = 0 then you get a pure greedy search.

It’s hard to give a general rule for what value to set, because it’s highly dependent on the distribution of distances in the dataset and that is determined by the distance metric and the dimensionality of the data itself. I recommend leaving this as the default, and only modifying it if you find that the search is unreasonably slow (in which case make epsilon smaller) or unreasonably inaccurate (in which case make epsilon larger). Yes, not very helpful I know. In the benchmarking done in (Dobson et al. 2023) using a similar back-tracking method, epsilon = 0.25 was the maximum value used and in (Wang et al. 2021) epsilon = 0.1 was used.

`init`

This controls how the search is initialized. If you don’t provide this, then k random neighbors per item in query will be generated for you.

Neighbor Graph Input

You may provide your own input for this. It should be in the neighbor graph format, i.e. a list of two matrices, idx and dist, as described above. Make sure that the dist matrix contains the distances using the same metric you will use in the search.

Neighbor Indices Only

In fact, the dist matrix is optional. If you only provide the idx matrix, then the dist matrix will be calculated for you. If the dist matrix is already available to you and it was generated by rnndescent then there is no reason not to use it, but you could have neighbors that come from:

another nearest neighbor package and for some reason you don’t have the distance
or you have indices from a different metric that you nonetheless believe are a good guess for the “real” metric.

A case where this might be worth experimenting with could be if you can cheaply binarize your input data, i.e. convert it to 0/1 then to FALSE/TRUE: you could then use the hamming metric or another binary-specialized metric on that input data. Even a brute force search can be very fast on this data. This could be a good way to get a good guess for the real data.

This is a very contrived example with iris, but let’s do it anyway:

numeric_iris <- iris[, sapply(iris, is.numeric)]
logical_iris <- sweep(numeric_iris, 2, colMeans(numeric_iris), ">")
logical_iris_even <- logical_iris[seq_len(nrow(logical_iris)) %% 2 == 0, ]
logical_iris_odd <- logical_iris[seq_len(nrow(logical_iris)) %% 2 == 1, ]
head(logical_iris_even)
#>      Sepal.Length Sepal.Width Petal.Length Petal.Width
#> [1,]        FALSE       FALSE        FALSE       FALSE
#> [2,]        FALSE        TRUE        FALSE       FALSE
#> [3,]        FALSE        TRUE        FALSE       FALSE
#> [4,]        FALSE        TRUE        FALSE       FALSE
#> [5,]        FALSE        TRUE        FALSE       FALSE
#> [6,]        FALSE        TRUE        FALSE       FALSE

Do a brute force search on the binarized data:

iris_logical_brute_nbrs <- brute_force_knn_query(
  query = logical_iris_odd,
  reference = logical_iris_even,
  k = 15,
  metric = "hamming"
)

Then pass the indices of the brute force search to graph_knn_query, which will generate the Euclidean distances for you:

graph_nbrs <- graph_knn_query(
  query = iris_odd,
  reference = iris_even,
  reference_graph = rpf_nbrs,
  init = iris_logical_brute_nbrs$idx,
  k = 15
)

Whether this is worth doing all depends on whether the time taken to binarize the data followed by the initial search on the binary data (it doesn’t have to be brute force) gives you a good enough guess to save time in the “real” search with graph_knn_query.

Forest initialization

If you have previously built an RP Forest with the data you may also use that to initialize the query. We can re-use rpf_index here.

forest_init_nbrs <- graph_knn_query(
  query = iris_odd,
  reference = iris_even,
  reference_graph = rpf_nbrs,
  init = rpf_index,
  k = 15
)

In general, the RP forest initialization is likely to be a better initial guess than random, but in terms of a speed/accuracy trade-off, using a large forest may not be the best choice. You may want to use rpf_filter to reduce the size of the forest before using it as an initial guess. In the PyNNDescent Python package that rnndescent is based on, only one tree is used for initializing query results.

Preparing the Search Graph

In all the examples so far, we have used the k-nearest neighbors graph as the reference_graph input to graph_knn_query. Is this actually a good idea? Probably not! There is no guarantee that all the items in the original dataset can actually be reached via the k-nearest neighbors graph. Some nodes just aren’t very popular and may not be in the neighbor list of any other item. That means you can never reach them via the k-nearest neighbors graph, no matter how thoroughly you search it.

We can solve this problem by reversing all the edges in the graph and adding them to the graph. So if you can get to item i from item j, you can now get to item j from item i. This solves one problem but adds some more which is that just like some items are very unpopular, other items might be very popular and appear often in the neighbor list of other items. Having a large number of these edges in the graph can make the search very slow. We therefore need to prune some of these edges.

prepare_search_graph is a function that will take a k-nearest neighbor graph and add edges to it to make it more useful for a search. The procedure is based on the process described in (Harwood and Drummond 2016) and consists of:

Reversing all the edges in the graph.
“Diversifying” the graph by “occlusion pruning”. This considers triplets of points, and removes long edges which are probably redundant. For an item $i$ with neighbors $p$ and $q$ if the distances $d_{pq} \lt d_{ip}$ i.e. the neighbors are closer to each other than they are to $i$ , then it is said that $p$ occludes $q$ and we don’t need both edges $i \rightarrow p$ and $i \rightarrow q$ – it’s likely that $q$ is in the neighbor list of $p$ or vice versa, so it’s unlikely that we are doing any harm by getting rid of $i \rightarrow p$ .
After occlusion pruning, if any item still has an excessive number of edges, the longest edges are removed until the number of edges is below the threshold.

To control all this pruning the following parameters are available:

Diversification Probability

diversify_prob is the probability of a neighbor being removed if it is found to be an “occlusion”. This should take a value between 0 (no diversification) and 1 (remove as many edges as possible). The default is 1.0.

The DiskAnn/Vamana method’s pruning algorithm is almost identical but instead of a probability, uses a related parameter called alpha, which acts in the opposite direction: increasing alpha increases the density of the graph. Why am I telling you this? The pbbsbench implementation of PyNNDescent uses alpha instead of diversify_prob and in the accompanying paper (Dobson et al. 2023) they mention that the use of alpha yields “modest improvements” – from context this seems to mean relative to using diversify_prob = 1.0. I can’t give an exact mapping between the two values unfortunately.

Degree Pruning

pruning_degree_multiplier controls how many edges to remove after the occlusion pruning relative to the number of neighbors in the original nearest neighbor graph. The default is 1.5 which means to allow as many as 50% more edge than the original graph. So if the input graph was for k = 15, each item in the search graph will have at most 15 * 1.5 = 22 edges.

Let’s see how this works on the iris neighbors:

set.seed(42)
iris_search_graph <- prepare_search_graph(
  data = iris_even,
  graph = rpf_nbrs,
  diversify_prob = 0.1,
  pruning_degree_multiplier = 1.5
)

Because the returned search graph can contain different number of edges per item, the neighbor graph format isn’t suitable. Instead you get back a sparse matrix, specifically a dgCMatrix. Here’s a histogram of how the edges are distributed:

search_graph_edges <- diff(iris_search_graph@p)
hist(search_graph_edges,
  main = "Distribution of search graph edges", xlab = "# edges"
)

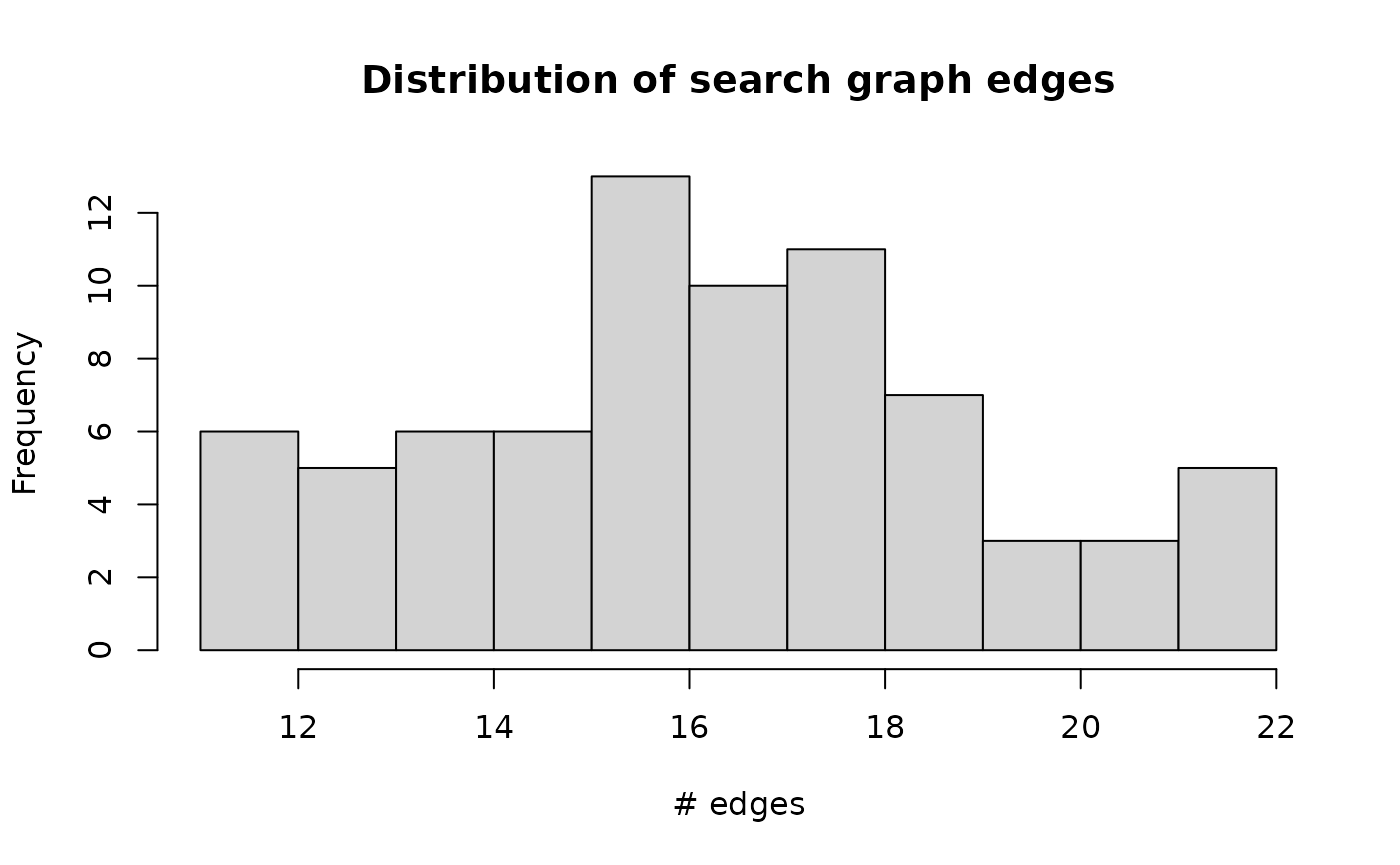
range(search_graph_edges)
#> [1] 11 22

So most items have around about k = 15 edges just like the nearest neighbor graph. But some have have the maximum number of edges and few have only 10 edges.

search_nbrs <- graph_knn_query(
  query = iris_odd,
  reference = iris_even,
  reference_graph = iris_search_graph,
  init = rpf_index,
  k = 15
)

References

Dobson, Magdalen, Zheqi Shen, Guy E Blelloch, Laxman Dhulipala, Yan Gu, Harsha Vardhan Simhadri, and Yihan Sun. 2023. “Scaling Graph-Based ANNS Algorithms to Billion-Size Datasets: A Comparative Analysis.” arXiv Preprint arXiv:2305.04359.

Harwood, Ben, and Tom Drummond. 2016. “Fanng: Fast Approximate Nearest Neighbour Graphs.” In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 5713–22.

Iwasaki, Masajiro, and Daisuke Miyazaki. 2018. “Optimization of Indexing Based on k-Nearest Neighbor Graph for Proximity Search in High-Dimensional Data.” arXiv Preprint arXiv:1810.07355.

Wang, Mengzhao, Xiaoliang Xu, Qiang Yue, and Yuxiang Wang. 2021. “A Comprehensive Survey and Experimental Comparison of Graph-Based Approximate Nearest Neighbor Search.” arXiv Preprint arXiv:2101.12631.